
【题目】如图,在△ABC中,AB=AC=10,点D是边BC上一动点(不与B、C重合),∠ADE=∠B=α,DE交AC于点E,且cosα= ![]() ,则线段CE的最大值为 .
,则线段CE的最大值为 . 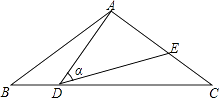
【答案】6.4
【解析】解:作AG⊥BC于G,如图,
∵AB=AC,
∴BG=CG,
∵∠ADE=∠B=α,
∴cosB=cosα= ![]() =
= ![]() ,
,
∴BG= ![]() ×10=8,
×10=8,
∴BC=2BG=16,
设BD=x,则CD=16﹣x,
∵∠ADC=∠B+∠BAD,即α+∠CDE=∠B+∠BAD,
∴∠CDE=∠BAD,
而∠B=∠C,
∴△ABD∽△DCE,
∴ ![]() =
= ![]() ,即
,即 ![]() =
= ![]() ,
,
∴CE=﹣ ![]() x2+
x2+ ![]() x
x
=﹣ ![]() (x﹣8)2+6.4,
(x﹣8)2+6.4,
当x=8时,CE最大,最大值为6.4.
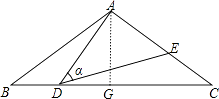
作AG⊥BC于G,如图,根据等腰三角形的性质得BG=CG,再利用余弦的定义计算出BG=8,则BC=2BG=16,设BD=x,则CD=16﹣x,证明△ABD∽△DCE,利用相似比可表示出CE=﹣ ![]() x2+
x2+ ![]() x,然后利用二次函数的性质求CE的最大值.
x,然后利用二次函数的性质求CE的最大值.


 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ABC=90°,D是边AC上一点,连接BD,使∠A=2∠1,点E是BC上的一点,以BE为直径的⊙O经过点D.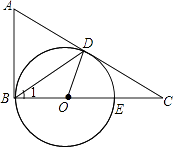
(1)求证:AC是⊙O的切线;
(2)若∠A=60°,⊙O的半径为2,求AB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把正方体的6个面分别涂上不同的颜色,并画上朵数不等的花,各面上的颜色与花朵数的情况如下表:
颜色 | 红 | 黄 | 蓝 | 白 | 紫 | 绿 |
花朵数 | 1 | 2 | 3 | 4 | 5 | 6 |
现将上述大小相同,颜色、花朵分布完全一样的四个正方体拼成一个在同一平面上放置的长方体,如图所示,那么长方体的下底面共有_____朵花.
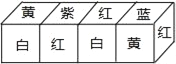
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】等腰三角形ABC在平面直角坐标系中的位置如图所示,已知点A(﹣6,0),点B在原点,CA=CB=5,把等腰三角形ABC沿x轴正半轴作无滑动顺时针翻转,第一次翻转到位置①,第二次翻转到位置②…依此规律,第15次翻转后点C的横坐标是 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小聪和小明沿同一条笔直的马路同时从学校出发到某图书馆查阅资料,学校与 图书馆的路程是 ![]() 千米,小聪骑自行车,小明步行,当小聪从原路回到学校时,小明刚好到 达图书馆,图中折线
千米,小聪骑自行车,小明步行,当小聪从原路回到学校时,小明刚好到 达图书馆,图中折线 ![]() 和线段
和线段 ![]() 分别表示两人离学校的路程
分别表示两人离学校的路程 ![]() (千米)与所经过的 时间
(千米)与所经过的 时间 ![]() (分钟)之间的函数关系,请根据图像回答下列问题:
(分钟)之间的函数关系,请根据图像回答下列问题:
(1)小聪在图书馆查阅资料的时间为 分钟;小聪返回学校的速度为 千米/分钟.
(2)请你求出小明离开学校的路程 ![]() (千米)与所经过的时间
(千米)与所经过的时间 ![]() (分钟)之间的函数表达式;
(分钟)之间的函数表达式;
(3)若设两人在路上相距不超过 ![]() 千米时称为可以“互相望见”,则小聪和小明可以“互相 望见”的时间共有多少分钟?
千米时称为可以“互相望见”,则小聪和小明可以“互相 望见”的时间共有多少分钟?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小王剪了两张直角三角形纸片,进行了如下的操作:
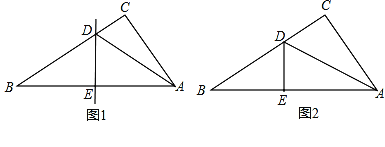
操作一:如图1,将Rt△ABC沿某条直线折叠,使斜边的两个端点A与B重合,折痕为DE.
(1)如果AC=6cm,BC=8cm,可求得△ACD的周长为 ;
(2)如果∠CAD:∠BAD=4:7,可求得∠B的度数为 ;
操作二:如图2,小王拿出另一张Rt△ABC纸片,将直角边AC沿直线AD折叠,使它落在斜边AB上,且与AE重合,若AC=9cm,BC=12cm,请求出CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,A、B两点分别在x轴、y轴上,OA=3,OB=4,连接AB.点P在平面内,若以点P、A、B为顶点的三角形与△AOB全等(点P与点O不重合),则点P的坐标为 . 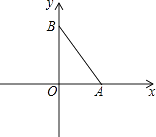
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=-![]() x+3
x+3![]() 的图像分别与x轴、y轴交于A、B两点.动点P从A点开始沿折线AO-OB-BA运动,点P在AO,OB,BA上运动的速度分别为1,
的图像分别与x轴、y轴交于A、B两点.动点P从A点开始沿折线AO-OB-BA运动,点P在AO,OB,BA上运动的速度分别为1,![]() ,2 (长度单位/秒);动点E从O点开始以
,2 (长度单位/秒);动点E从O点开始以![]() (长度单位/秒)的速度沿线段OB运动.设P、E两点同时出发,运动时间为t (秒),当点P沿折线AO-OB-BA运动一周时,动点E和P同时停止运动.过点E作EF∥OA,交AB于点F.
(长度单位/秒)的速度沿线段OB运动.设P、E两点同时出发,运动时间为t (秒),当点P沿折线AO-OB-BA运动一周时,动点E和P同时停止运动.过点E作EF∥OA,交AB于点F.
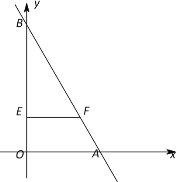
(1)求线段AB的长;
(2)求证:∠ABO=30°;
(3)当t为何值时,点P与点E重合?
(4)当t = 时,PE=PF .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知数轴上点A表示的数为8,B是数轴上一点,且AB=14.
![]()
(1)写出数轴上点B表示的数;
(2)若点M、N分别是线段AO、BO的中点,求线段MN的长;
(3)若动点P从点A出发.以每秒5个单位长度的速度沿数轴向左匀速运动,动点Q从点B出发,以每秒3个单位长度的速度沿数轴向左匀速运动,若点P、Q同时出发.问点P运动多少秒时追上点Q?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com