
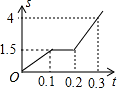
 某学生每天早晨骑自行车上学,早晨7点准时出发,以某一速度匀速前进.一天早上,由于有事,停下耽误了几分钟为了按时到校,他加快了速度,仍匀速前进,结果准点到校.这位同学这天早上7点出发的路程S(千米)与时间t(小时)的函数图象如图所示,则这位同学准点到校的时间为
某学生每天早晨骑自行车上学,早晨7点准时出发,以某一速度匀速前进.一天早上,由于有事,停下耽误了几分钟为了按时到校,他加快了速度,仍匀速前进,结果准点到校.这位同学这天早上7点出发的路程S(千米)与时间t(小时)的函数图象如图所示,则这位同学准点到校的时间为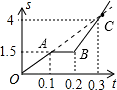 解:设OA的解析式为y=kx,
解:设OA的解析式为y=kx,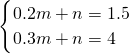 ,
,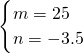 ,
,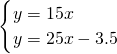 ,
,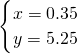 .
.

科目:初中数学 来源: 题型:解答题
 已知在矩形ABCD中.
已知在矩形ABCD中.查看答案和解析>>
科目:初中数学 来源: 题型:单选题
 如图,要测量水池AB的宽,先在空地处取一点O,使点A、O、D与点B、O、C都分别在同一直线上,量得OA=OD,OB=OC,这时,CD的长就是AB的长.这是根据全等三角形的对应边相等得到的,三角形全等的理由是
如图,要测量水池AB的宽,先在空地处取一点O,使点A、O、D与点B、O、C都分别在同一直线上,量得OA=OD,OB=OC,这时,CD的长就是AB的长.这是根据全等三角形的对应边相等得到的,三角形全等的理由是查看答案和解析>>
科目:初中数学 来源: 题型:单选题
查看答案和解析>>
科目:初中数学 来源: 题型:单选题
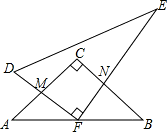 一副三角板如图摆放,点F是45°角三角板ABC的斜边的中点,AC=4.当30°角三角板DEF的直角顶点绕着点F旋转时,直角边DF,EF分别与AC,BC相交于点M,N.在旋转过程中有以下结论:①MF=NF:②四边形CMFN有可能为正方形;③MN长度的最小值为2;④四边形CMFN的面积保持不变;⑤△CMN面积的最大值为2.其中正确的个数是
一副三角板如图摆放,点F是45°角三角板ABC的斜边的中点,AC=4.当30°角三角板DEF的直角顶点绕着点F旋转时,直角边DF,EF分别与AC,BC相交于点M,N.在旋转过程中有以下结论:①MF=NF:②四边形CMFN有可能为正方形;③MN长度的最小值为2;④四边形CMFN的面积保持不变;⑤△CMN面积的最大值为2.其中正确的个数是查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,AD、AM、AH分别△ABC的角平分线、中线和高.
如图,AD、AM、AH分别△ABC的角平分线、中线和高. ∠________;
∠________; ________;
________;查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com