
【题目】如图,已知△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是边BC中点,两边PE、PF分别交AB、AC于点E、F,当∠EPF在△ABC内绕顶点P旋转时(点E不与A、B重合),给出以下四个结论:①AE=CF;②△EPF是等腰直角三角形;③四边形AEPF的面积=△ABC的面积的一半,④当EF最短时,EF=AP,上述结论始终正确的个数为( )

A. 1 B. 2 C. 3 D. 4
【答案】D
【解析】
根据等腰直角三角形的性质可得∠BAP=∠C=45°,AP=CP,根据等角的余角相等求出∠APE=∠CPF,然后利用“角边角”证明△AEP和△CPF全等,根据全等三角形对应边相等可得AE=CF,PE=PF,全等三角形的面积相等求出S四边形AEPF=S△APC,然后解答即可.
∵AB=AC,∠BAC=90°,∴△ABC是等腰直角三角形.
∵点P为BC的中点,∴∠BAP=∠C=45°,AP=CP.
∵∠EPF是直角,∴∠APE+∠APF=∠CPF+∠APF=90°,∴∠APE=∠CPF.
在△AEP和△CPF中,∵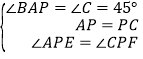 ,∴△AEP≌△CPF(ASA),∴AE=CF,PE=PF,S△APE=S△CPF,∴S四边形AEPF=S△APC,∴S四边形AEPF=
,∴△AEP≌△CPF(ASA),∴AE=CF,PE=PF,S△APE=S△CPF,∴S四边形AEPF=S△APC,∴S四边形AEPF=![]() S△ABC,根据等腰直角三角形的性质,EF=
S△ABC,根据等腰直角三角形的性质,EF=![]() PE,所以,EF随着点E的变化而变化,只有当点E为AB的中点时,EF=
PE,所以,EF随着点E的变化而变化,只有当点E为AB的中点时,EF=![]() PE=AP,此时,EF最短;故①②③④正确.
PE=AP,此时,EF最短;故①②③④正确.
故选D.


科目:初中数学 来源: 题型:
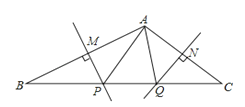
【题目】如图,在△ABC中,AB的垂直平分线分别交AB、BC于点M、P,AC的垂直平分线分别交AC、BC于点N、Q,∠BAC=110°,则∠PAQ=_____°.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠A=60°,∠B=58°.甲、乙两人想在△ABC外部取一点D,使得△ABC与△DCB全等,其作法如下:
(甲)①作∠A的角平分线L.
②以B为圆心,BC长为半径画弧,交L于D点,则D即为所求.
(乙)①过B作平行AC的直线L.
②过C作平行AB的直线M,交L于D点,则D即为所求.
对于甲、乙两人的作法,下列判断何者正确?( )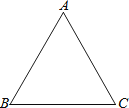
A.两人皆正确
B.两人皆错误
C.甲正确,乙错误
D.甲错误,乙正确
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一个安装有进出水管的30升容器,水管每单位时间内进出的水量是一定的,设从某时刻开始的4分钟内只进水不出水,在随后的8分钟内既进水又出水,得到水量![]() (升)与时间
(升)与时间![]() (分)之间的函数关系如图所示.根据图象回答下列问题:
(分)之间的函数关系如图所示.根据图象回答下列问题:
(1)求每分钟进水多少升;
(2)若12分钟后只放水,不进水,求需要多长时间可以把水放完;
(3)若从一开始进出水管同时打开,求需要多长时间可以将容器灌满。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,∠B=30°,以点A为圆心,任意长为半径画弧分别交AB,AC于点M和N,再分别以点M,N为圆心,大于![]() MN的长为半径画弧,两弧交于点P,连接AP并延长交BC于点D,则下列说法:①AD是∠BAC的平分线;②∠ADC=60°;③点D在AB的垂直平分线上;④S△DAC:S△ABC=1:3.其中正确的是__________________.(填所有正确说法的序号)
MN的长为半径画弧,两弧交于点P,连接AP并延长交BC于点D,则下列说法:①AD是∠BAC的平分线;②∠ADC=60°;③点D在AB的垂直平分线上;④S△DAC:S△ABC=1:3.其中正确的是__________________.(填所有正确说法的序号)

查看答案和解析>>
科目:初中数学 来源: 题型:
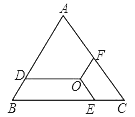
【题目】如图O是边长为9的等边三角形ABC内的任意一点,且OD∥BC,交AB于点D,OF∥AB,交AC于点F,OE∥AC,交BC于点E,则OD+OE+OF的值为( )
A. 3 B. 6 C. 8 D. 9
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知二次函数y1=ax2+bx+c的图象过点A(1,0),B(﹣3,0),C(0,﹣3) 
(1)求此二次函数的解析式和顶点坐标;
(2)直线y2=kx+b过B、C两点,请直接写出当y1>y2时,自变量x的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com