
【题目】已知点P(2x,3x-1)是平面直角坐标系上的点。
(1)若点P在第一象限的角平分线上,求x的值;
(2)若点P在第三象限,且到两坐标轴的距离之和为16,求x的值。
科目:初中数学 来源: 题型:
【题目】如图,点A(0,8),点B(4,0),连接AB,点M,N分别是OA,AB的中点,在射线MN上有一动点P.若△ABP是直角三角形,则点P的坐标是__.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(9分) “先学后教”课题组对学生参与小组合作的深度和广度进行评价,其评价项目为主动质疑、独立思考、专注听讲、讲解题目四项.课题组随机抽取了若干名初中学生的参与情况,绘制了如图两幅不完整的统计图,请根据图中所给信息解答下列问题:

(1)在这次评价中,一共抽查了______名学生;
(2)请将条形统计图补充完整;
(3)求出扇形统计图中,“主动质疑”所对应扇形的圆心角的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】张老师每天从甲地到乙地锻炼身体,甲、乙两地相距14千米,已知他步行的平均速度为80米/分,跑步的平均速度为200米/分,若他要在不超过10分钟的时间内从甲地到达乙地,至少需要跑步多少分钟?设他需要跑步x分钟,则列出的不等式( )
A.80x+200(10-x)≤1.4B.80x+200(10-x)≤1400
C.200x+80(10-x)≥1.4D.200x+80(10-x)≥1400
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AD∥BC,E是AB的中点,连接DE并延长交CB的延长线于点F,点G在边BC上,且∠GDF=∠ADF.

(1)求证:△ADE≌△BFE;
(2)连接EG,判断EG与DF的位置关系并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
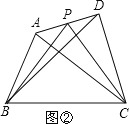
【题目】提出问题:如图①,在四边形ABCD中,P是AD边上任意一点,
△PBC与△ABC和△DBC的面积之间有什么关系?
探究发现:为了解决这个问题,我们可以先从一些简单的、特殊的情形入手:
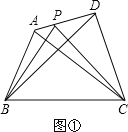
(1)当AP=![]() AD时(如图②):
AD时(如图②):
∵AP=![]() AD,△ABP和△ABD的高相等,
AD,△ABP和△ABD的高相等,
∴S△ABP=![]() S△ABD.
S△ABD.
∵PD=AD﹣AP=![]() AD,△CDP和△CDA的高相等,
AD,△CDP和△CDA的高相等,
∴S△CDP=![]() S△CDA.
S△CDA.
∴S△PBC=S四边形ABCD﹣S△ABP﹣S△CDP
=S四边形ABCD﹣![]() S△ABD﹣
S△ABD﹣![]() S△CDA
S△CDA
=S四边形ABCD﹣![]() (S四边形ABCD﹣S△DBC)﹣
(S四边形ABCD﹣S△DBC)﹣![]() (S四边形ABCD﹣S△ABC)
(S四边形ABCD﹣S△ABC)
=![]() S△DBC+
S△DBC+![]() S△ABC.
S△ABC.
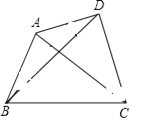
(2)当AP=![]() AD时,探求S△PBC与S△ABC和S△DBC之间的关系,写出求解过程;
AD时,探求S△PBC与S△ABC和S△DBC之间的关系,写出求解过程;
(3)当AP=![]() AD时,S△PBC与S△ABC和S△DBC之间的关系式为: ;
AD时,S△PBC与S△ABC和S△DBC之间的关系式为: ;
(4)一般地,当AP=![]() AD(n表示正整数)时,探求S△PBC与S△ABC和S△DBC之间的关系,写出求解过程;
AD(n表示正整数)时,探求S△PBC与S△ABC和S△DBC之间的关系,写出求解过程;
问题解决:当AP=![]() AD(0≤
AD(0≤![]() ≤1)时,S△PBC与S△ABC和S△DBC之间的关系式为: .
≤1)时,S△PBC与S△ABC和S△DBC之间的关系式为: .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】王霞和爸爸、妈妈到人民公园游玩,回到家后,她利用平面直角坐标系画出了公园的景区地图,如图所示.可是她忘记了在图中标出原点和x轴.y轴.只知道游乐园D的坐标为(2,﹣2),请你帮她画出坐标系,并写出其他各景点的坐标.
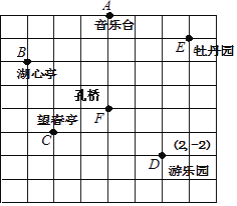
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com