
����Ŀ����ͼ1�����ǰѶԽ����ഹֱ���ı��ν��������ı��Σ�
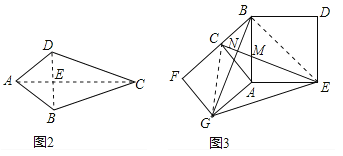
��1���������⣺��ͼ2�����ı���ABCD�У�AB=AD��CB=CD�����ı���ABCD�Ǵ����ı�������˵�����ɣ�
��2������̽������̽�������ı���ABCD����Ա�AB��CD��BC��AD֮���������ϵ��
������ۣ���Ҫ������������������ д��֤�����̣��Ȼ���ͼ�Σ�д����֪����֤����
��3������������ͼ3���ֱ���Rt��ACB��ֱ�DZ�AC��б��ABΪ��������������ACFG��������ABDE������CE��BG��GE����֪AC=4��AB=5����GE����

���𰸡���1���ı���ABCD�Ǵ����ı�������2�������ı��ε�����Աߵ�ƽ�����������3��![]() ��
��
��������
�����������1�����ݴ�ֱƽ���ߵ��ж�����֤�����ɣ�
��2�����ݴ�ֱ�Ķ�����ɶ�����ɣ�
��3�����ݴ����ı��ε����ʡ����ɶ�������ϣ�2���Ľ��ۼ��㣮
�����������1���ı���ABCD�Ǵ����ı��Σ�
֤������AB=AD�����A���߶�BD�Ĵ�ֱƽ�����ϣ���CB=CD�����C���߶�BD�Ĵ�ֱƽ�����ϣ���ֱ��AC���߶�BD�Ĵ�ֱƽ���ߣ���AC��BD�����ı���ABCD�Ǵ����ı��Σ�
��2��������ۣ������ı��ε�����Աߵ�ƽ������ȣ�
��ͼ2����֪�ı���ABCD�У�AC��BD������ΪE����֤��![]() .
.
֤������AC��BD�����AED=��AEB=��BEC=��CED=90�㣬�ɹ��ɶ����ã�![]() =
=![]() ��
��![]() =
=![]() ����
����![]() ��
��
��3������CG��BE���ߡ�CAG=��BAE=90�㣬���CAG+��BAC=��BAE+��BAC������GAB=��CAE���ڡ�GAB�͡�CAE�У���AG=AC����GAB=��CAE��AB=AE�����GAB�ա�CAE�����ABG=��AEC���֡�AEC+��AME=90�㣬���ABG+��AME=90�㣬��CE��BG�����ı���CGEB�Ǵ����ı��Σ��ɣ�2���ã�![]() ����AC=4��AB=5����BC=3��CG=
����AC=4��AB=5����BC=3��CG=![]() ��BE=
��BE=![]() ����
����![]() =73����GE=
=73����GE=![]() ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������x��һԪ���η���x2��kx��2��0��һ����Ϊ��1������һ����Ϊ_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������ӯ��5%������+5%����ô��3%��ʾ��������
A.����3%
B.����8%
C.ӯ��2%
D.��3%
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1��������ABCD�У�AB=![]() ��tan��ABC=2����E�ӵ�D��������ÿ��1����λ���ȵ��ٶ���������DA�ķ��������˶������˶�ʱ��Ϊt���룩�����߶�CE�Ƶ�C˳ʱ����תһ���Ǧ�����=��BCD�����õ���Ӧ�߶�CF��
��tan��ABC=2����E�ӵ�D��������ÿ��1����λ���ȵ��ٶ���������DA�ķ��������˶������˶�ʱ��Ϊt���룩�����߶�CE�Ƶ�C˳ʱ����תһ���Ǧ�����=��BCD�����õ���Ӧ�߶�CF��
��1����֤��BE=DF��
��2����t= ��ʱ��DF�ij�������Сֵ����Сֵ���� ��
��3����ͼ2������BD��EF��BD��EC��EF�ڵ�P��Q����tΪ��ֵʱ����EPQ��ֱ�������Σ�
��4����ͼ3�����߶�CD�Ƶ�C˳ʱ����תһ���Ǧ�����=��BCD�����õ���Ӧ�߶�CG���ڵ�E���˶������У������Ķ�Ӧ��Fλ��ֱ��AD�Ϸ�ʱ��ֱ��д����F��ֱ��AD�ľ���y����ʱ��t�ĺ�������ʽ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����Ķ����в��ϣ��������Ӧ������
���������Ҷ���
�����£�archimedes����Ԫǰ287����Ԫǰ212�꣬��ϣ��������ʷ������ΰ�����ѧ��֮һ������ţ�١���˹����Ϊ������ѧ���ӣ�
������Al��Binmi��973��1050�꣩�������б����˰��������Ҷ��������ݣ�������1964�����Al��Binmi�뱾�����˶��İ桶������ȫ��������һ����ǰ��������Ҷ�����
���������Ҷ�������ͼ1��AB��BC����O�������ң�������ABC��Բ��һ�����ң���BC��AB��M��![]() ���е㣬���M��BC�������ߵĴ���D������ABC���е㣬��CD=AB+BD�����������á��س�����֤��CD=AB+BD�IJ���֤�����̣�֤������ͼ2����CB�Ͻ�ȡCG=AB������MA��MB��MC��MG��
���е㣬���M��BC�������ߵĴ���D������ABC���е㣬��CD=AB+BD�����������á��س�����֤��CD=AB+BD�IJ���֤�����̣�֤������ͼ2����CB�Ͻ�ȡCG=AB������MA��MB��MC��MG��
��M��![]() ���е㣬��MA=MC��
���е㣬��MA=MC��
��
����
��1���밴�������֤��˼·��д����֤����ʣ�ಿ�֣�
��2����գ���ͼ3����֪�ȱ���ABC�ڽ�����O��AB=2��DΪ![]() ��һ�㣬��ABD=45�㣬AE��BD�ڵ�E������BDC���ܳ��� ��
��һ�㣬��ABD=45�㣬AE��BD�ڵ�E������BDC���ܳ��� ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������Ϧ��͡Ϧ»������ҡϦ����Ϧ£������б�ʾ�Ϧµ���ǵ�ʽ���У���90�㩁�Ϧ£��ڡϦ���90�㣻�� ![]() ���Ϧ�+�Ϧ£�����
���Ϧ�+�Ϧ£����� ![]() ���Ϧ����Ϧ£�����ȷ���У� ��
���Ϧ����Ϧ£�����ȷ���У� ��
A.4��
B.3��
C.2��
D.1��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У�AB=AC��DΪBC����һ�㣬��B=30�㣬��DAB=45�㣮 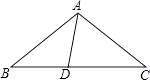
��1�����DAC�Ķ�����
��2����֤��DC=AB��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com