
| A. | x=1,y=3 | B. | x=4,y=1 | C. | x=3,y=2 | D. | x=2,y=3 |
分析 根据金属棒的长度是40cm,则可以得到7x+9y≤40,再根据x,y都是正整数,即可求得所有可能的结果,分别计算出省料的长度即可确定.
解答 解:根据题意得:7x+9y≤40,
则x≤$\frac{40-9y}{7}$,
∵40-9y≥0且y是正整数,
∴y的值可以是:1或2或3或4.
当y=1时,x≤$\frac{31}{7}$,则x=4,此时,所剩的废料是:40-1×9-4×7=3cm;
当y=2时,x≤$\frac{22}{7}$,则x=3,此时,所剩的废料是:40-2×9-3×7=1cm;
当y=3时,x≤$\frac{13}{7}$,则x=1,此时,所剩的废料是:40-3×9-7=6cm;
当y=4时,x≤$\frac{4}{7}$,则x=0(舍去).
则最小的是:x=3,y=2.
故选C.
点评 本题考查了不等式的应用,读懂题意,列出算式,正确确定出x,y的所有取值情况是本题的关键.


科目:初中数学 来源: 题型:选择题
| A. | 1:3 | B. | 3:1 | C. | 1:$\sqrt{3}$ | D. | $\sqrt{3}$:1 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
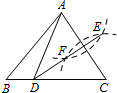 如图,在△ABC中,分别以点A、C为圆心,以大于$\frac{AC}{2}$长为半径作圆弧,两弧分别相交于点E、F,连结EF并延长交边BC于点D,连结AD.若AB=6,BC=8,则△ABD的周长为( )
如图,在△ABC中,分别以点A、C为圆心,以大于$\frac{AC}{2}$长为半径作圆弧,两弧分别相交于点E、F,连结EF并延长交边BC于点D,连结AD.若AB=6,BC=8,则△ABD的周长为( )| A. | 8 | B. | 10 | C. | 12 | D. | 14 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{15}{2}$ | B. | $\frac{3}{2}$($\sqrt{7}$+4) | C. | 6 | D. | $\frac{3}{2}$(4±$\sqrt{7}$) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,小明沿着一个斜坡从坡底A向坡顶B行走的过程中发现,他毎向前走60m,他的高度就升高36m,则这个斜坡的坡度等于1:$\frac{4}{3}$.
如图,小明沿着一个斜坡从坡底A向坡顶B行走的过程中发现,他毎向前走60m,他的高度就升高36m,则这个斜坡的坡度等于1:$\frac{4}{3}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com