练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    15．己知一次函数y=kx-5和y=k′x+3，假设k＞0，k′＜0，则这两个一次函数图象的交点在第一或四象限．

    分析 根据一次函数的解析式画出函数图象，根据一次函数图象与系数的关系结合图形即可得出结论．

    解答 解：分别作出一次函数y=kx-5和y=k′x+3的图象，如图所示．
    ∵在一次函数y=kx-5中，k＞0，-5＜0，
    ∴该一次函数图象过第一、三、四象限；
    ∵在一次函数y=k′x+3中，k′＜0，3＞0，
    ∴该一次函数图象过第一、二、四象限．
    ∴这两个一次函数图象的交点可能在第一或第四象限．
    故答案为：一或四．

    点评 本题考查了两条直线相交或平行问题以及一次函数图象与系数的关系，根据一次函数图象与系数的关系画出函数图象是解题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    5．有些大数值问题可以通过用字母代替数转化成整式问题来解决，请先阅读下面的解题过程，再解答下面的问题．
    例：若x=123456789×123456786，y=123456788×123456787，试比较x、y的大小．
    解：设123456788=a，那么x=（a+1）（a-2）=a2-a-2，y=a（a-1）=a2-a，
    ∵x-y=（a2-a-2）-（a2-a）=-2，∴x＜y
    看完后，你学到了这种方法吗？再亲自试一试吧，你准行！
    问题：若x=20072007×20072011-20072008×20072010，
    y=20072008×20072012-20072009×20072011，若设20072007=a，试用类似方法比较x、y的大小．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    6．已知2x=3，2y=5，则22x-y-1的值是$\frac{9}{10}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    3．如图1，已知直线y=$\frac{2}{5}$x+2与x轴交于点A，与y轴交于点C，抛物线y=ax2+4ax+b经过A．C两点，且与x轴交于另一点B．

    （1）求抛物线的解析式；
    （2）若点Q在抛物线上，且△AQC与△BQC面积相等，求点Q的坐标；
    （3）如图2，P为△AOC外接圆上弧ACO的中点，直线PC交x轴于点D，∠EDF=∠ACO，当∠EDF绕点D旋转时，DE交直线AC于点M，DF交y轴负半轴于点N．请你探究：CN-CM的值是否发生变化？若不变，求出其值；若变化，求出变化范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

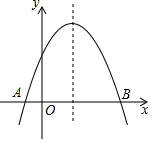    10．函数y=-x2+2（m-1）x+m+1的图象如图，它与x轴交于A，B两点，线段OA与OB的比为1：3，则m的值为（　　）
    A．$\frac{1}{3}$或2B．$\frac{1}{3}$C．1D．2

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    20．如图所示，二次函数y=ax2+bx+c（a≠0）的图象与x轴相交于点A，B，若其对称轴为直线x=2，则OB-OA的值为4．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    7．某饭店所有员工的月收入情况如下：
    经理领班 迎宾　厨师厨师助理　服务员
    　人数（人）122238
    　月收入（元）6700 3900　28004200　32003000　
    该饭店所有员工月收入的众数是3000元．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    15．（1）计算：（x-y）2-（y+2x）（y-2x）；
    （2）解方程：$\frac{5}{{x}^{2}+3x}$-$\frac{1}{{x}^{2}-x}$=0．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

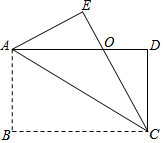    16．如图，四边形ABCD是矩形，把矩形沿对角线AC折叠，点B落在点E处，CE与AD相交于点O．
    （1）求证：EO=DO；
    （2）若∠OCD=30°，AB=$\sqrt{3}$，求△ACO的面积．

    查看答案和解析>>

    同步练习册答案