
分析 (1)根据六位连接数的定义可知123123为六位连接数,再将123123进行因数分解,判断得出它能被13整除;
(2)设$\overline{abc}$$\overline{abc}$为六位连接数,将$\overline{abc}$$\overline{abc}$进行因数分解,判断得出它能被13整除;
(3)设$\overline{xyxy}$为四位连接数,用含x、y的代数式表示M与N,再计算M-N,然后将$\frac{M-N}{13}$表示为77x+7y+$\frac{3x+4y}{13}$,根据M-N的结果能被13整除以及M与N都是1~9之间的整数,求得x与y的值,即可求解.
解答 解:(1)123123为六位连接数;
∵123123=123×1001=123×13×77,
∴123123能被13整除;
(2)任意六位连接数都能被13整除,理由如下:
设$\overline{abc}$$\overline{abc}$为六位连接数,
∵$\overline{abc}$$\overline{abc}$=$\overline{abc}$×1001=$\overline{abc}$×13×77,
∴$\overline{abc}$$\overline{abc}$能被13整除;
(3)设$\overline{xyxy}$为四位连接数,
则M=1000x+100y+10x+y=1010x+101y,N=3(x+y+x+y)=6x+6y,
∴M-N=(1010x+101y)-(6x+6y)=1004x+95y,
∴$\frac{M-N}{13}$=$\frac{1004x+95y}{13}$=77x+7y+$\frac{3x+4y}{13}$,
∵M-N的结果能被13整除,
∴$\frac{3x+4y}{13}$是整数,
∵M与N都是1~9之间的整数,
∴x=1,y=9;x=2,y=5;x=3,y=1;
∴这样的四位连接数有1919,2525,3131,一共3个.
点评 本题考查了因式分解的应用,整式的运算,理解“连接数”的定义是解题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ①②③④ | B. | ②③④ | C. | ②③ | D. | ①③ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
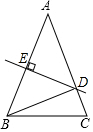 如图,在△ABC中,DE是边AB的垂直平分线,交AB于E、交AC于D,连接BD.
如图,在△ABC中,DE是边AB的垂直平分线,交AB于E、交AC于D,连接BD.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com