
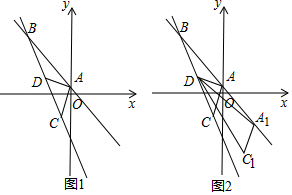
分析 (1)先求点A的坐标,根据三角形面积公式可知:$\frac{1}{2}$|xB|•OA=3,可得B的横坐标为:-6,因为点B是第二象限一次函数y=-x+1的图象上一点,可得B的坐标;
(2)构建梯形,则S△ABC=S梯形ABEF-S△ACF-S△BEC代入可得面积;利用三角形中线的性质:将面积分为相等的两部分,反之,可知:D是BC的中点,利用中点坐标公式或构建直角三角形得
点D的坐标;
(3)根据一次函数y=-x+1设A1的坐标,根据平移规律表示点C1的坐标,当△A1C1D直角三角形时,分三个顶点分别是直角顶点这三种情况进行讨论,利用勾股定理列方程可得x的值,求A1的坐标.
解答 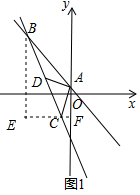 解:(1)∵一次函数y=-x+1的图象与y轴交于点A,
解:(1)∵一次函数y=-x+1的图象与y轴交于点A,
∴当x=0时,y=1,
∴点A的坐标为(0,1),
∴OA=1
∵S△OAB=3,
∴$\frac{1}{2}$|xB|•OA=3,
∴|xB|=6,
∵点B是第二象限一次函数y=-x+1的图象上一点,
∴B的横坐标为:-6,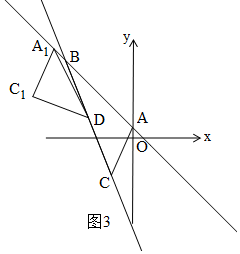
则y=-(-6)+1=7,
∴点B的坐标为:(-6,7);
(2)如图1,过点B作BE⊥x轴,过点C作CF⊥y轴于点F,交BE于点E,
∵点C的坐标为(-2,-3),
∴BE=10,EF=6,EC=4,CF=2,AF=4,
∴S△ABC=S梯形ABEF-S△ACF-S△BEC=$\frac{1}{2}$×(4+10)×6-$\frac{1}{2}$×4×2-$\frac{1}{2}$×10×4=18;
∵点D是线段BC上一点,且三角形ABD的面积是三角形ABC的一半,
∴点D是BC的中点,
∴点D的坐标为:(-4,2);
(3)如图2,∵A(0,1),C(-2,-3),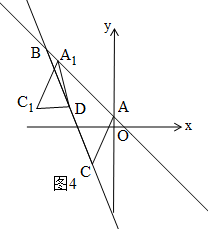
∴由平移可知:点C是点A向左平移2个单位,再向下平移4个单位所得,
设A1(x,-x+1),则C1(x-2,-x+1-4),即(x-2,-x-3),
当△A1C1D直角三角形时,分三种情况:
①当∠DA1C1=90°时,如图2,由勾股定理得:${A}_{1}{D}^{2}+{A}_{1}{{C}_{1}}^{2}$=$D{{C}_{1}}^{2}$,
∴(x+4)2+(-x+1-2)2+(x-2-x)2+(-x-3+x-1)2=(x-2+4)2+(-x-3-2)2
解得:x=2,
∴A1(2,-1);
②当∠A1C1D=90°时,如图3,由勾股定理得:${A}_{1}{{C}_{1}}^{2}+{C}_{1}{D}^{2}={A}_{1}{D}^{2}$,
∴(x-2-x)2+(-x-3+x-1)2+(x-2+4)2+(-x-3-2)2=(x+4)2+(-x+1-2)2,
解得:x=-8,
∴A1(-8,9);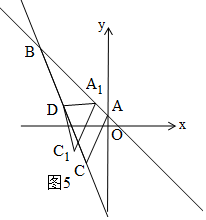
③当∠A1DC1=90°时,如图4和图5,由勾股定理得:A1D2+C1D2=A1C12,
∴(x+4)2+(-x+1-2)2+(x-2+4)2+(-x-3-2)2=(x-2-x)2+(-x-3+x-1)2,
2x2+12x+13=0,
解得:x=$\frac{-6±\sqrt{10}}{2}$,
∴A1($\frac{-6+\sqrt{10}}{2}$,$\frac{8-\sqrt{10}}{2}$)或($\frac{-6-\sqrt{10}}{2}$,$\frac{8+\sqrt{10}}{2}$);
综上所述,点A1的坐标为:(2,-1)或(-8,9)或($\frac{-6+\sqrt{10}}{2}$,$\frac{8-\sqrt{10}}{2}$)或($\frac{-6-\sqrt{10}}{2}$,$\frac{8+\sqrt{10}}{2}$).
点评 本题是一次函数的综合题,考查了一次函数与坐标轴的交点、三角形面积、平移的原则、勾股定理、中点坐标公式,第三问有难度,利用平移规律得出C1的坐标是关键,并采用了分类讨论的思想,与方程相结合,解决问题.


 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
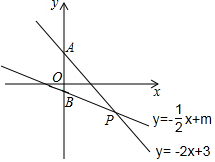 如图,函数y=-2x+3与y=-$\frac{1}{2}$x+m的图象交于(n,-2).
如图,函数y=-2x+3与y=-$\frac{1}{2}$x+m的图象交于(n,-2).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com