
����Ŀ����ͼ��������y=ax2+bx��a��b��a��0��a��bΪ��������x�ύ��A��C���㣬��y�ύ��B�㣬ֱ��AB�ĺ�����ϵʽΪy=![]() x+
x+![]() ��
��
��1����������ߵĺ�����ϵʽ��C�����ꣻ
��2����֪��M��m��0�����߶�OA�ϵ�һ�����㣬����M��x��Ĵ���l�ֱ���ֱ��AB�������߽���D��E���㣬��mΪ��ֵʱ����BDEǡ������DEΪ�ױߵĵ��������Σ�
��3���ڣ�2���������£�����BDEǡ������DEΪ�ױߵĵ���������ʱ������M��Ӧλ�ü�Ϊ��M�䣬��OM����ԭ��O˳ʱ����ת�õ�ON����ת����0�㵽90��֮�䣩��
i��̽�����߶�OB���Ƿ���ڶ���P��P����O��B�غϣ�������ON�����ת��![]() ʼ�ձ��ֲ��䣬�����ڣ������P�����ꣻ�������ڣ���˵�����ɣ�
ʼ�ձ��ֲ��䣬�����ڣ������P�����ꣻ�������ڣ���˵�����ɣ�
ii�����������ת�����У���NA+![]() NB������Сֵ��
NB������Сֵ��

���𰸡���1�������ߵĺ�����ϵʽΪ��y=��![]() x2��
x2��![]() x+
x+![]() ��C��1��0������2����m=��4ʱ����BDEǡ������DEΪ�ױߵĵ��������Σ�(3). ���ڣ����ɼ���������NA+
��C��1��0������2����m=��4ʱ����BDEǡ������DEΪ�ױߵĵ��������Σ�(3). ���ڣ����ɼ���������NA+![]() NB������СֵΪ
NB������СֵΪ![]() .
.
��������
�����������1��������֪�����õ�B��0��![]() ����A����6��0�����ⷽ����õ������ߵĺ�����ϵʽΪ��y=��
����A����6��0�����ⷽ����õ������ߵĺ�����ϵʽΪ��y=��![]() x2��
x2��![]() x+
x+![]() �����ǵõ�C��1��0������2���ɵ�M��m��0��������M��x��Ĵ���l�ֱ���ֱ��AB�������߽���D��E���㣬�õ�D��m��
�����ǵõ�C��1��0������2���ɵ�M��m��0��������M��x��Ĵ���l�ֱ���ֱ��AB�������߽���D��E���㣬�õ�D��m��![]() m+
m+![]() ������DEΪ��ʱ����BG��DE��G�����ݵ��������ε����ʵõ�EG=GD=
������DEΪ��ʱ����BG��DE��G�����ݵ��������ε����ʵõ�EG=GD=![]() ED��GM=OB=
ED��GM=OB=![]() ���з��̼��ɵõ����ۣ���3��i��������֪�����õ�ON=OM��=4��OB=
���з��̼��ɵõ����ۣ���3��i��������֪�����õ�ON=OM��=4��OB=![]() ���ɡ�NOP=��BON������ĵ���NOP�ס�BONʱ���������������ε����ʵõ�
���ɡ�NOP=��BON������ĵ���NOP�ס�BONʱ���������������ε����ʵõ�![]() =
=![]() �����ǵõ����ۣ�ii����������õ�N����OΪԲ�ģ�4Ϊ�뾶�İ�Բ�ϣ��ɣ�i��֪��
�����ǵõ����ۣ�ii����������õ�N����OΪԲ�ģ�4Ϊ�뾶�İ�Բ�ϣ��ɣ�i��֪��![]() =
=![]() ���õ�NP=
���õ�NP=![]() NB�����ǵõ���NA+
NB�����ǵõ���NA+![]() NB������Сֵ=NA+NP����ʱN��A��P���㹲�ߣ����ݹ��ɶ����õ����ۣ�
NB������Сֵ=NA+NP����ʱN��A��P���㹲�ߣ����ݹ��ɶ����õ����ۣ�
���������
��1����y=![]() x+
x+![]() ����x=0����y=
����x=0����y=![]() ����y=0����x=��6����B��0��
����y=0����x=��6����B��0��![]() ����A����6��0����
����A����6��0����
��B��0��![]() ����A����6��0������y=ax2+bx��a��b��
����A����6��0������y=ax2+bx��a��b��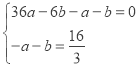 ��
��
��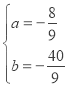 ���������ߵĺ�����ϵʽΪ��y=��
���������ߵĺ�����ϵʽΪ��y=��![]() x2��
x2��![]() x+
x+![]() ��
��
��y=0����=��![]() x2��
x2��![]() x+
x+![]() =0����x1=��6��x2=1����C��1��0����
=0����x1=��6��x2=1����C��1��0����
��2���ߵ�M��m��0��������M��x��Ĵ���l�ֱ���ֱ��AB�������߽���D��E���㣬
��D��m��![]() m+
m+![]() ������DEΪ��ʱ��
������DEΪ��ʱ��
��BG��DE��G����EG=GD=![]() ED��GM=OB=
ED��GM=OB=![]() ��
��
��![]() m+
m+![]() +
+![]() ����
����![]() m2��
m2��![]() +
+![]() +
+![]() m+
m+![]() ��=
��=![]() ��
��
��ã�m1=��4��m2=9���������⣬��ȥ����
�൱m=��4ʱ����BDEǡ������DEΪ�ױߵĵ��������Σ�
��3��i�����ڣ�
��ON=OM��=4��OB=![]() ����NOP=��BON��
����NOP=��BON��
�൱��NOP�ס�BONʱ��![]() =
=![]() ��
��
��![]() ���䣬��OP=
���䣬��OP=![]() =3����P��0��3��
=3����P��0��3��
ii����N����OΪԲ�ģ�4Ϊ�뾶�İ�Բ�ϣ��ɣ�i��֪��![]() =
=![]() ��
��
��NP=![]() NB���ࣨNA+
NB���ࣨNA+![]() NB������Сֵ=NA+NP�����ʱN��A��P���㹲�ߣ�
NB������Сֵ=NA+NP�����ʱN��A��P���㹲�ߣ�
�ࣨNA+![]() NB������Сֵ=
NB������Сֵ=![]() ,
,


 Сѧ��10���ӿ������100��ϵ�д�
Сѧ��10���ӿ������100��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ���˻������У��������ִ�Ⱦ���֪�ڶ��α���Ⱦ����420�ˣ����ÿ�ִ�Ⱦ�ʶ���ͬ����ôÿ�ִ�Ⱦ��ƽ��һ���˴�Ⱦ��________���ˣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ij��ѧ�С��Ϊ����ѧУ���AB�ĸ߶ȣ��������ǰ��![]() �״��ĵ�C����,��б���¶�
�״��ĵ�C����,��б���¶�![]() ��б��CDǰ��4�����D���ڵ�D�����ò���ǣ������˶���A������Ϊ37�������������ĸ�DEΪ1.5��.��֪A��B��C��D��E��ͬһƽ���ڣ�AB��BC,AB//DE.�����AB�ĸ߶�.���ο����ݣ�sin37����
��б��CDǰ��4�����D���ڵ�D�����ò���ǣ������˶���A������Ϊ37�������������ĸ�DEΪ1.5��.��֪A��B��C��D��E��ͬһƽ���ڣ�AB��BC,AB//DE.�����AB�ĸ߶�.���ο����ݣ�sin37����![]() ��cos37����
��cos37����![]() ��tan37����
��tan37����![]() .�������������ţ�
.�������������ţ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����P(2����3)���ڵ������ǣ� ��
A. ��һ����B. �ڶ�����C. ��������D. ��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ��ʱ����604800�룬��604800�ÿ�ѧ��������ʾΪ��������
A.60.48��104B.6.048��106C.6.048��105D.0.6048��105
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�й�������ͨ����ͨ��Ϊ��Ӧ����������ɫ���С��ĺ��٣���ס�³ǵ�С���ϰ����Լݳ���Ϊ��������������֪С���Ҿ��ϰ�ص�18ǧ�ף����ó˹������ķ�ʽƽ��ÿСʱ��ʻ��·�̱������Լݳ��ķ�ʽƽ��ÿСʱ��ʻ��·�̵�2������9ǧ�ף����Ӽҳ��������ϰ�ص㣬�˹�������ʽ����ʱ�����Լݳ���ʽ����ʱ��� ![]() ��С�����Լݳ���ʽ�ϰ�ƽ��ÿСʱ��ʻ����ǧ�ף�
��С�����Լݳ���ʽ�ϰ�ƽ��ÿСʱ��ʻ����ǧ�ף�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������¼�Ϊ��Ȼ�¼����ǣ� ��
A.���ӣ����ڲ�������B.��һ�ŵ�ӰƱ����λ����������
C.��һö���ӣ�������������D.��һö�ʵؾ��ȵ�Ӳ�ң����泯��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ������3��4��x��6��7��������3�����������ݵ���λ��Ϊ��������
A.3B.4C.6D.7
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com