
【题目】在平面直角坐标系中,点A(m,m)在第一象限,且实数m满足条件:![]() ,ABy轴于B,ACx轴于C
,ABy轴于B,ACx轴于C
(1)求m的值;
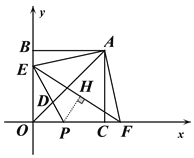
(2)如图1,BE=1,过A作AF⊥AE交x轴于F,连EF,D在AO上,且AD=AE,连接ED并延长交x轴于点P,求点P的坐标;
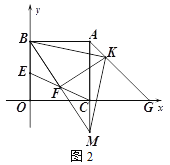
(3)如图2,G为线段OC延长线上一点,AC=CG,E为线段OB上一动点(不与O、B重合),F为线段CE的中点,若BF⊥FK交AG于K,延长BF、AC交于M,连接KM.请问∠FBK的大小是否变化?若不变,请求其值;若改变,求出变化的范围.

【答案】(1)7;(2)P(3,0);(3)∠FBK的大小不变,为45°,理由见解析.
【解析】
(1)由![]() 有意义可得m≥4,从而得到
有意义可得m≥4,从而得到![]() ,然后根据条件就可求出m的值.
,然后根据条件就可求出m的值.
(2)过点D作DH⊥x轴于点H,根据全等三角形的性质及勾股定理,就可得到点P的坐标.
(3)过K作KN⊥AC于N,KT⊥BA延长线于T.易证四边形ATKN是正方形,则有KT=KN,∠MTN=90°.易证△BEF≌△MCF,则有BF=MF,根据垂直平分线的性质可得KB=KM,从而可证到△TBK≌△NMK,进而得到答案.
(1)由![]() 得
得 ![]() ,
,![]() ,
,
∴![]() ,
,
原式化为:![]() ,
,
∴![]() ,
,
![]() .
.
(2)由(1)得A(7,7),
∵AB⊥y轴于B,AC⊥x轴于C,
∴AE=AC=7,
∴四边形ABOC为正方形,
∴BO=OC=7,∠BAC=90°,∠BOA=45°,
∵AF⊥AE,
∴∠EAF=90°,
∴∠BAE=∠CAF,
∴△ABE≌△ACF(ASA)
∴BE=CF,AE=AF,
∴∠AEF=45°,
∵AD=AE,
∴∠AED=∠ADE,
∴∠AEF+∠FEP=∠EOA+∠OEP,
∴∠OEP=∠FEP ,
过P作PH⊥EF于H,
∴OP=PH,
∴EO=EH,
在Rt△EOF中,EO=BO-BE=6,OF=OC+CF=8,
∴EF=![]() ,
,
设OP=PH=x,
在Rt△HPF中,HF=10-6=4,PF=8-x,
![]() ,即
,即![]() ,
,
解得![]() ,
,
∴P(3,0);
(3)∠FBK的大小不变,为45°。理由如下:
∵有正方形ABOC,
<>∴BO∥AC, ∠BAC=∠ACO=90°,∴∠EBF=∠CMF,∠BEF=∠MCF,
∵F为EC中点,
∴EF=CF,
∴△BEF≌△MCF(AAS),
∴BF=MF ,
∵BF⊥FK,
∴KB=KM ,
过K作KN⊥AC于N,KT⊥BA延长线于T,

∴∠T=∠KNM=90°,
∴四边形TANK为矩形,
∵AC=CG,
∴∠ANK=45°,
∴AN=NK,
∴矩形TANK为正方形,
∴TK=NK,
∴△TBK≌△NMK ,
∴∠TBK=∠NMK,
∴∠BKM=∠BAM=90°,
∴∠KBM=45°.


科目:初中数学 来源: 题型:
【题目】如图,已知点A(4,0),B(0,4 ![]() ),把一个直角三角尺DEF放在△OAB内,使其斜边FD在线段AB上,三角尺可沿着线段AB上下滑动.其中∠EFD=30°,ED=2,点G为边FD的中点.
),把一个直角三角尺DEF放在△OAB内,使其斜边FD在线段AB上,三角尺可沿着线段AB上下滑动.其中∠EFD=30°,ED=2,点G为边FD的中点.
(1)求直线AB的解析式;
(2)如图1,当点D与点A重合时,求经过点G的反比例函数y= ![]() (k≠0)的解析式;
(k≠0)的解析式;
(3)在三角尺滑动的过程中,经过点G的反比例函数的图象能否同时经过点F?如果能,求出此时反比例函数的解析式;如果不能,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,点A在函数 ![]() 的图象上,AB⊥
的图象上,AB⊥ ![]() 轴于点B,AB的垂直平分线与
轴于点B,AB的垂直平分线与 ![]() 轴交于点C,与函数
轴交于点C,与函数 ![]() 的图象交于点D。连结AC,CB,BD,DA,则四边形ACBD的面积等于( )
的图象交于点D。连结AC,CB,BD,DA,则四边形ACBD的面积等于( )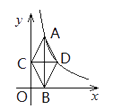
A. 2
B.![]()
C.4
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在矩形ABCD中,动点P从点B出发,沿BC,CD,DA运动至点A停止.设点P运动的路程为x,△ABP的面积为y,如果y关于x的函数图象如图2所示,则△ABC的面积是 ( )
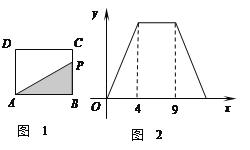
A. 10B. 16C. 18D. 20
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:如图1,抛物线 ![]() 与
与 ![]() 轴交于A,B两点,点P在抛物线上(点P与A,B两点不重合),如果△ABP的三边满足
轴交于A,B两点,点P在抛物线上(点P与A,B两点不重合),如果△ABP的三边满足 ![]() ,则称点P为抛物线
,则称点P为抛物线 ![]() 的勾股点。
的勾股点。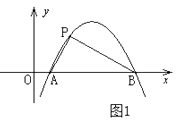
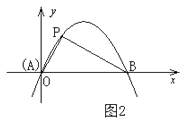
(1)直接写出抛物线 ![]() 的勾股点的坐标;
的勾股点的坐标;
(2)如图2,已知抛物线C: ![]() 与
与 ![]() 轴交于A,B两点,点P(1,
轴交于A,B两点,点P(1, ![]() )是抛物线C的勾股点,求抛物线C的函数表达式;
)是抛物线C的勾股点,求抛物线C的函数表达式;
(3)在(2)的条件下,点Q在抛物线C上,求满足条件 ![]() 的点Q(异于点P)的坐标
的点Q(异于点P)的坐标
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在全体丽水人民的努力下,我市剿灭劣V类水“河道清淤”工程取得了阶段性成果,下面的右表是全市十个县(市、区)指标任务数的统计表;左图是截止2017年3月31日和截止5月4日,全市十个县(市、区)指标任务累计完成数的统计图.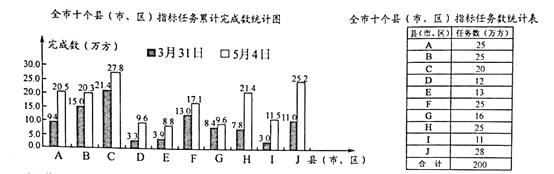
(1)截止3月31日,完成进度(完成进度=累计完成数÷任务数×100%)最快、电慢的县(市、区)分别是哪一个?
(2)求截止5月4日全市的完成进度;
(3)请结合图形信息和数据分析,对I且完成指标任务的行动过程和成果进行评价.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图A、B分别为数轴上的两点,A点对应的数为-10,B点对应的数为90.
![]()
(1)请写出与A,B两点距离相等的M点对应的数;
(2)现在有一只电子蚂蚁P从B点出发时,以3个单位/秒的速度向左运动,同时另一只电子蚂蚁Q恰好从A点出发,以2个单位/秒的速度向右运动,设两只电子蚂蚁在数轴上的C点相遇,求C点对应的数是多少.
(3)若当电子蚂蚁P从B点出发时,以3个单位/秒的速度向左运动,同时另一只电子蚂蚁Q恰好从A点出发,以2个单位/秒的速度向右运动,求经过多长的时间两只电子蚂蚁在数轴上相距35个单位长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系xOy中,已知A(6,0),B(8,6),将线段OA平移至CB,点D在x轴正半轴上(不与点A重合),连接OC,AB,CD,BD.
(1)写出点C的坐标;
(2)当△ODC的面积是△ABD的面积的3倍时,求点D的坐标;
(3)设∠OCD=α,∠DBA=β,∠BDC=θ,判断α、β、θ之间的数量关系,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com