
 等腰△ABC的顶角为36°,BC沿CD对折,点B交AC于E,求DE与AD的比值.
等腰△ABC的顶角为36°,BC沿CD对折,点B交AC于E,求DE与AD的比值. 分析 根据勾股定理、三角形内角和定理求出∠B、∠DCB的度数,证明△CDB∽△ABC,得到AD2=BD•BA,根据黄金分割的概念进行计算即可.
解答 解:∵∠A=36°,AB=AC,
∴∠B=∠ACB=72°,
∴∠DCA=∠DCB=36°,
∴△CDB∽△ABC,
∴BC2=BD•BA,
∵BC=CD=DA,
∴AD2=BD•BA,
∴D是AB的黄金分割点,
∴AD=$\frac{\sqrt{5}-1}{2}$AB,BD=$\frac{3-\sqrt{5}}{2}$AB,
∴$\frac{DE}{AD}$=$\frac{\sqrt{5}-1}{2}$.
点评 本题考查的是翻折变换的性质和黄金分割的概念,找准翻折变换中的对应边和对应角是解题的关键.


 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
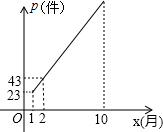 解放碑泰兴电脑城某店在1~10月份销售A、B两种电子产品,已知A产品每月的售价y(元)与月份x(1≤x≤10且x为整数)之间的关系可用如下表格表示:
解放碑泰兴电脑城某店在1~10月份销售A、B两种电子产品,已知A产品每月的售价y(元)与月份x(1≤x≤10且x为整数)之间的关系可用如下表格表示:| 时间x(月) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 售价y(元) | 720 | 360 | 240 | 180 | 144 | 120 | 120 | 120 | 120 | 120 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com