
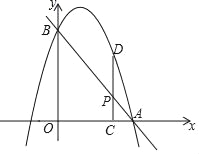
【题目】如图,已知直线y=﹣2x+4分别交x轴、y轴于点A、B,抛物线过A,B两点,点P是线段AB上一动点,过点P作PC⊥x轴于点C,交抛物线于点D.
(1)若抛物线的解析式为y=﹣2x2+2x+4,设其顶点为M,其对称轴交AB于点N.
①求点M、N的坐标;
②是否存在点P,使四边形MNPD为菱形?并说明理由;
(2)当点P的横坐标为1时,是否存在这样的抛物线,使得以B、P、D为顶点的三角形与△AOB相似?若存在,求出满足条件的抛物线的解析式;若不存在,请说明理由.
【答案】(1)①点N坐标为(![]() ,3);②不存在.理由见解析;(2)存在.满足条件的抛物线的解析式为y=﹣2x2+2x+4或y=﹣
,3);②不存在.理由见解析;(2)存在.满足条件的抛物线的解析式为y=﹣2x2+2x+4或y=﹣![]() x2+3x+4.
x2+3x+4.
【解析】
(1)①将抛物线配成顶点式可得到顶点坐标M![]() 再通过
再通过![]() 在对称轴上求出N的坐标;
在对称轴上求出N的坐标;
②易得![]() ,通过将点P,点D的坐标设出来可得
,通过将点P,点D的坐标设出来可得![]() ,由PD∥MN,可知PD=MN时,四边形MNPD是平行四边形;求
,由PD∥MN,可知PD=MN时,四边形MNPD是平行四边形;求![]() 值后通过比较
值后通过比较![]() 与
与![]() 的大小可判断四边形MNPD是否为菱形;
的大小可判断四边形MNPD是否为菱形;
(2)先由点P的坐标求出![]() ,然后将抛物线解析式设为y=ax2+bx+4,再由
,然后将抛物线解析式设为y=ax2+bx+4,再由![]() 得到
得到![]() ,求出
,求出![]() 由∠DPB=∠OBA,可对相似三角形进行分类讨论,分别求出
由∠DPB=∠OBA,可对相似三角形进行分类讨论,分别求出![]() 值即可.
值即可.
(1)①如图1,
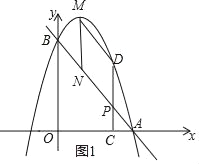
![]()
∴顶点为M的坐标为![]()
当![]() 时,
时,![]() ,则点N坐标为
,则点N坐标为![]()
②不存在.
理由如下:
![]()
设P点坐标为![]() ,则
,则![]()
∴![]()
∵PD∥MN,
当PD=MN时,四边形MNPD为平行四边形,即![]() 解得
解得![]() (舍去),
(舍去),![]() 此时P点坐标为
此时P点坐标为![]()
∵![]()
∴PN≠MN,
∴平行四边形MNPD不为菱形,
∴不存在点P,使四边形MNPD为菱形;
(2)存在.
如图2,
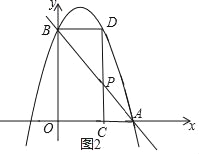
OB=4,OA=2,则![]()
当x=1时,y=﹣2x+4=2,则P(1,2),
∴![]()
设抛物线的解析式为y=ax2+bx+4,
把A(2,0)代入得4a+2b+4=0,解得b=﹣2a﹣2,
∴抛物线的解析式为y=ax2﹣2(a+1)x+4,
当x=1时,y=ax2﹣2(a+1)x+4=a﹣2a﹣2+4=2﹣a,则D(1,2﹣a),
∴![]()
∵DC∥OB,
∴∠DPB=∠OBA,
∴当![]() 时,△PDB∽△BOA,即
时,△PDB∽△BOA,即![]() ,解得
,解得![]() ,此时抛物线解析式为
,此时抛物线解析式为![]()
当![]() 时,△PDB∽△BAO,即
时,△PDB∽△BAO,即![]() ,解得
,解得![]() ,此时抛物线解析式为
,此时抛物线解析式为![]()
综上所述,满足条件的抛物线的解析式为![]() 或
或![]()


 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案科目:初中数学 来源: 题型:
【题目】小明在学习了正方形之后,给同桌小文出了道题,从下列四个条件:①AB=BC,②∠ABC=90°,③AC=BD,④AC⊥BD中选两个作为补充条件,使ABCD为正方形(如图),现有下列四种选法,你认为其中错误的是( )

A.①②B.②③C.①③D.②④
查看答案和解析>>
科目:初中数学 来源: 题型:
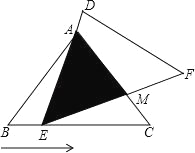
【题目】如图,在△ABC中,已知AB=AC=5,BC=6,且△ABC≌△DEF,将△DEF与△ABC重合在一起,△ABC不动,△DEF运动,并满足:点E在边BC上沿B到C的方向运动,且DE始终经过点A,EF与AC交于M点.
(1)求证:△ABE∽△ECM;
(2)探究:在△DEF运动过程中,重叠部分能否构成等腰三角形?若能,求出BE的长;若不能,请说明理由;
(3)当线段BE为何值时,线段AM最短,最短是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点C是⊙O优弧ACB上的中点,弦AB=6cm,E为OC上任意一点,动点F从点A出发,以每秒1cm的速度沿AB方向响点B匀速运动,若y=AE-EF,则y与动点F的运动时间x(0≤x≤6 )秒的函数关系式为 .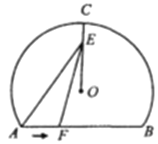
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等边三角形ABC中,点P是BC边上一动点(不与点B、C重合),连接AP,作射线PD,使∠APD=60°,PD交AC于点D,已知AB=a,设CD=y,BP=x,则y与x函数关系的大致图象是( )

A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
科目:初中数学 来源: 题型:
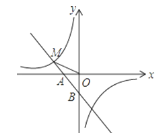
【题目】如图,一次函数y1=﹣x﹣1的图象与x轴交于点A,与y轴交于点B,与反比例函数y2=![]() 图象的一个交点为M(﹣2,m).
图象的一个交点为M(﹣2,m).
(1)求反比例函数的解析式;
(2)求△MOB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
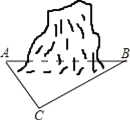
【题目】为促进我市经济的快速发展,加快道路建设,某高速公路建设工程中需修隧道AB,如图,在山外一点C测得BC距离为200m,∠CAB=54°,∠CBA=30°,求隧道AB的长.(参考数据:sin54°≈0.81,cos54°≈0.59,tan54°≈1.38, ![]() ≈1.73,精确到个位)
≈1.73,精确到个位)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知线段a=0.3m,b=60cm,c=12dm.
(1)求线段a与线段b的比.
(2)如果线段a、b、c、d成比例,求线段d的长.
(3)b是a和c的比例中项吗?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(6分)株洲五桥主桥主孔为拱梁钢构组合体系(如图1),小明暑假旅游时,来到五桥观光,发现拱梁的路面部分有均匀排列着9根支柱,他回家上网查到了拱梁是抛物线,其跨度为20米,拱高(中柱)10米,于是他建立如图2的坐标系,发现可以将余下的8根支柱的高度都算出来了,请你求出中柱左边第二根支柱CD的高度.


查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com