
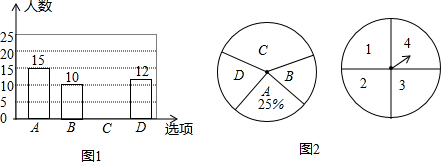
分析 (1)由A的人数及其人数占被调查人数的百分比可得样本容量;根据各项目人数之和等于总数,可得C选项的人数;
(2)用样本中最想去森林公园的学生人数占被调查人数的比例乘总人数即可得到该校最想去森林公园的学生人数;
(3)根据转盘画出树状图,依据所得的结果,进行计算即可得到小军获胜的概率.
解答 解:(1)本次调查的样本容量是:15÷25%=60;
补全条形统计图如下:
故答案为:60;
(2)该校最想去森林公园的学生人数为:
3600×$\frac{12}{60}$=720;
(3)画树状图如下: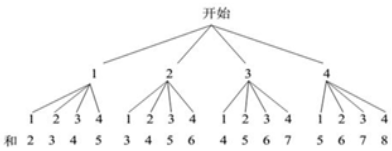
共有16种等可能的结果,其中和为5的结果有4种,
因此小军获胜的概率为$\frac{4}{16}$=$\frac{1}{4}$.
点评 本题主要考查了概率的计算,用样本估计总体,条形统计图以及扇形统计图的综合应用,解题时注意:树形图列举法一般是选择一个元素再和其他元素分别组合,依次列出,象树的枝丫形式,最末端的枝丫个数就是总的可能的结果n.当有两个元素时,可用树形图列举,也可以列表列举.


 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{3}{4}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
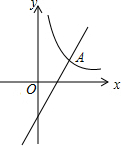 如图,已知一次函数y=kx-4k+5的图象与反比例函数y=$\frac{3}{x}$(x>0)的图象相交于点A(p,q).当一次函数y的值随x的值增大而增大时,p的取值范围是$\frac{3}{5}$<p<4.
如图,已知一次函数y=kx-4k+5的图象与反比例函数y=$\frac{3}{x}$(x>0)的图象相交于点A(p,q).当一次函数y的值随x的值增大而增大时,p的取值范围是$\frac{3}{5}$<p<4.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com