
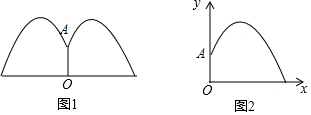 ������һ��Բ����ˮ�أ���ˮ�����봹ֱ��ˮ�氲װһ����������OA��Oǡ����ˮ�����ģ����������Ӷ���A������ͷ������ˮ��ˮ���ڸ�������������״��ͬ��������·�����£����ڹ�OA����ƽ���ϵ���������ͼ1��ʾ������ֱ������ϵ��ͼ2��ˮ������ĸ߶ȣ�m����ˮ�����x��m��֮��ĺ�����ϵʽ��y=a��x-h��2+k����OA=1.25m��ˮ������OAΪ1m����ʱ�����߶�2.25m����ش��������⣺
������һ��Բ����ˮ�أ���ˮ�����봹ֱ��ˮ�氲װһ����������OA��Oǡ����ˮ�����ģ����������Ӷ���A������ͷ������ˮ��ˮ���ڸ�������������״��ͬ��������·�����£����ڹ�OA����ƽ���ϵ���������ͼ1��ʾ������ֱ������ϵ��ͼ2��ˮ������ĸ߶ȣ�m����ˮ�����x��m��֮��ĺ�����ϵʽ��y=a��x-h��2+k����OA=1.25m��ˮ������OAΪ1m����ʱ�����߶�2.25m����ش��������⣺���� ��1��������֪�ó����κ����Ķ������꣬�������ö���ʽ�ó����κ�������ʽ����y=0����-��x-1��2+2.25=0�����x��ֵ���ɵó��𰸣���
��2����ˮ���������������״�루1����ͬ����a=-1����x=3.5ʱ��y=0����������𰸼��ɣ�
��� �⣺��1���߶���Ϊ��1��2.25����
�������ʽΪy=a��x-1��2+2.25���㣨0��1.25����
���a=-1��
���Խ���ʽΪ��y=-��x-1��2+2.25��
��y=0��
��-��x-1��2+2.25=0��
���x=2.5 ��x=-0.5����ȥ����
����ˮ�صİ뾶����Ҫ2.5�ײ���ʹ�����ˮ�������䵽���⣻
��2�������������������״�루1����ͬ�������������Ϊy=-x2+bx+c��
�ѵ㣨0��1.25����3.5��0��
��$\left\{\begin{array}{l}{c=1.25}\\{-\frac{49}{4}+\frac{7}{2}b+c=0}\end{array}\right.$��
��ã�$\left\{\begin{array}{l}{b=\frac{22}{7}}\\{c=\frac{5}{4}}\end{array}\right.$��
��y=-x2+$\frac{22}{7}$x+$\frac{5}{4}$=-��x-$\frac{11}{7}$��2+$\frac{729}{196}$��
��ˮ�صİ뾶Ϊ3.5m��Ҫʹˮ�����䵽���⣬��ʱˮ�����߶�Ӧ��$\frac{729}{196}$�ף�
���� ������Ҫ�����˶��κ�����Ӧ�ã����ݶ���ʽ������κ����Ľ���ʽ�ǽ���ؼ���


 ��Ǭ����������ҵ���ּ����ӱ����������ϵ�д�
��Ǭ����������ҵ���ּ����ӱ����������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��������ABCD��EF�۵����õ���ͼ��ʾ��ͼ�Σ���֪��BEF=50�㣬���AEB��Ĵ�С��80�ȣ�
��������ABCD��EF�۵����õ���ͼ��ʾ��ͼ�Σ���֪��BEF=50�㣬���AEB��Ĵ�С��80�ȣ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��AD��BC��BO��CO�ֱ�ƽ�֡�ABC����DCB����A+��D=m�����BOC�Ķ������ú�m�Ĵ���ʽ��ʾ��
��ͼ��AD��BC��BO��CO�ֱ�ƽ�֡�ABC����DCB����A+��D=m�����BOC�Ķ������ú�m�Ĵ���ʽ��ʾ���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��֪ʵ��a��b�������ϵ�λ����ͼ��ʾ���Ի���$\frac{a}{a-b}$$\sqrt{\frac{{a}^{2}b-2a{b}^{2}+{b}^{3}}{a}}$��
��֪ʵ��a��b�������ϵ�λ����ͼ��ʾ���Ի���$\frac{a}{a-b}$$\sqrt{\frac{{a}^{2}b-2a{b}^{2}+{b}^{3}}{a}}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com