
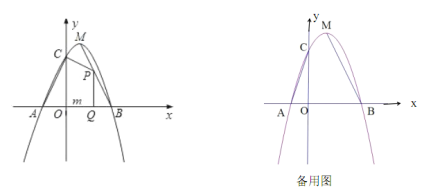
【题目】如图,已知二次函数![]() (
(![]() )的图象与
)的图象与![]() 轴交于
轴交于![]() 两点(点
两点(点![]() 在点
在点![]() 的左侧),与
的左侧),与![]() 轴交于点
轴交于点![]() ,且
,且![]() ,
,![]() ,顶点为
,顶点为![]() .
.
(1)求二次函数的解析式;
(2)点![]() 为线段
为线段![]() 上的一个动点,过点
上的一个动点,过点![]() 作
作![]() 轴的垂线
轴的垂线![]() ,垂足为
,垂足为![]() ,若
,若![]() ,四边形
,四边形![]() 的面积为
的面积为![]() ,求
,求![]() 关于
关于![]() 的函数解析式,并写出
的函数解析式,并写出![]() 的取值范围;
的取值范围;
(3)探索:线段![]() 上是否存在点
上是否存在点![]() ,使
,使![]() 为直角三角形?如果存在,求出点
为直角三角形?如果存在,求出点![]() 的坐标;如果不存在,请说明理由.
的坐标;如果不存在,请说明理由.
 综合自测系列答案
综合自测系列答案科目:初中数学 来源: 题型:
【题目】大熊山某农家乐为了抓住“五一”小长假的商机,决定购进A、B两种纪念品。若购进A种纪念品4件,B种纪念品3件,需要550元;若购进A种纪念品8件,B种纪念品5件,需要1050元。
(1)求购进A、B两种纪念品每件各需多少元。
(2)若该农家乐决定购进这两种纪念品共100件,考虑市场需求和资金周转,用于购买这100件纪念品的资金不少于7500元,但不超过7650元,那么该农家乐共有几种进货方案。
(3)若销售每件A种纪念品可获利润30元,每件B种纪念品可获利润20元,在第(2)问的各种进货方案中,哪一种方案获利最大?最大利润是多少元。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】铜仁市积极推动某公园建设,通过旅游带动一方经济,计划经过若干年使公园绿化总面积新增450万平方米.自2016年初开始实施后,实际每年绿化面积是原计划的1.5倍,这样可以提前3年完成任务.
(1)求实际每年绿化面积是多少万平方米
(2)为加大公园绿化力度,市政府决定从2019年起加快绿化速度,要求不超过2年完成,那么实际平均每年绿化面积至少还要增加多少万平方米?
查看答案和解析>>
科目:初中数学 来源: 题型:
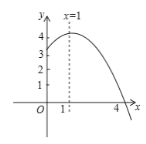
【题目】抛物线![]() (
(![]() )的部分图象如图所示,与
)的部分图象如图所示,与![]() 轴的一个交点坐标为
轴的一个交点坐标为![]() ,抛物线的对称轴是
,抛物线的对称轴是![]() ,下列结论是:①
,下列结论是:①![]() ;②
;②![]() ;③方程
;③方程![]() 有两个不相等的实数根;④
有两个不相等的实数根;④![]() ;⑤若点
;⑤若点![]() 在该抛物线上,则
在该抛物线上,则![]() ,其中正确的个数有( )
,其中正确的个数有( )
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
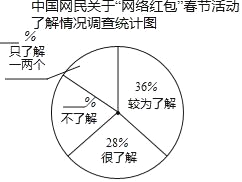
【题目】“网络红包”是互联网运营商、商家通过组织互联网线上活动、派发红包的互联网工具,是朋友间互道祝福的表达形式之一.“网络红包”春节活动已经逐渐深入到大众的生活中,得到了人们较为广泛的关注.根据某咨询公司(2018年中国春节“网络红包”专题调查报告》显示:在接受调查的8万名网民中,对“网络红包”春节话动了解程度的占比方面,“较为了解”和“很了解”的网民共占比64%,分别占比36%和28%.在“不了解”和“只了解一两个“的受访网民中,“不了解”的网民人数比“只了解一两个”的网民人数多25%.如图是该咨询公司绘制的“中国网民关于‘网络红包’春节活动了解情况调查”统计图(不完整).
请根据以上信息解答下列问题:
(1)在受访的网民中,“不了解”和“只了解一两个”的网民人数共有 万人,其中“不了解”的网民人数是 万人;
(2)请将扇形统计图补充完整;
(3)2017除夕晚上小聪和爸爸、妈妈一起玩微信抢红包游戏,他们约定由爸爸在家人微信群中先后发两次“拼手气红包”,每次发放的红包数是3个,每个红包抽到的金额随机(每两个红包的金额都不相等),每次谁抽到红包的金额最大谁就是“手气最佳”者,求两次游戏中小聪都能获得“手气最佳”的概率为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
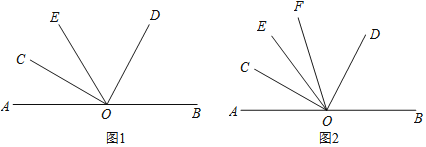
【题目】点O为直线AB上一点,在直线AB上侧任作一个∠COD,使∠COD=90°.
(1)如图1,过点O作射线OE,使OE是∠AOD的角平分线,求证:∠BOD=2∠COE;
(2)如图2,过点O作射线OE,使OC是∠AOE的角平分线,另作射线OF,使OF是∠COD的平分线,若∠EOC=3∠EOF,求∠AOE的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,对角线AC,BD相交于点O,∠ADB=30°,E为BC边上一点,∠AEB=45°,CF⊥BD于F.下列结论:①BE=CD,②BF=3DF,③AE=![]() AO,④CE=CF.正确的结论有( )
AO,④CE=CF.正确的结论有( )
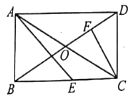
A. ①②B. ②③C. ①②④D. ①②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC的中线BD,CE交于点O,F,G分别是BO,CO的中点.
(1)填空:四边形DEFG是 四边形.
(2)若四边形DEFG是矩形,求证:AB=AC.
(3)若四边形DEFG是边长为2的正方形,试求△ABC的周长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC 的面积为 63,D 是 BC 上的一点,且 BD:BC=2:3, DE∥AC 交 AB 于点 E,延长 DE 到 F,使 FE:ED=2:1.连结 CF 交 AB 点于 G.
(1)求△BDE 的面积;
(2)求 ![]() 的值;
的值;
(3)求△ACG 的面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com