
【题目】某段公路经测算发现,匀速行驶的车辆通过该段公路时,所需时间t(h)与行驶速度v(km/h)满足反比例函数关系,其图象为如图所示的一段曲线.且端点为A(40,1)和B(m,0.5).
(1)求t与v的函数关系式及m的值;
(2)若该段公路限速50km/h,求通过该路段需要的最短时间和这段公路的长.
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案科目:初中数学 来源: 题型:
【题目】游泳是一项深受青少年喜爱的体育活动,学校为了加强学生的安全意识,组织学生观看了纪实片“孩子,请不要私自下水”,并于观看后在本校的2000名学生中作了抽样调查.请根据下面两个不完整的统计图回答以下问题:
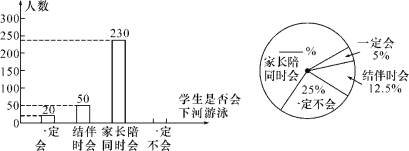
(1)这次抽样调查中,共调查了__ __名学生;
(2)补全两个统计图;
(3)根据抽样调查的结果,估算该校2000名学生中大约有多少人“一定会下河游泳”?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(8分)如图,在ABCD中,∠BCD=120°,分别延长DC、BC到点E,F,使得△BCE和△CDF都是正三角形.
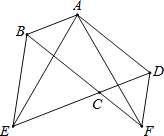
(1)求证:AE=AF;
(2)求∠EAF的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC中,∠A=60°,∠ACB=40°,D为BC边延长线上一点,BM平分∠ABC,E为射线BM上一点.若直线CE垂直于△ABC的一边,则∠BEC=____°.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平行四边形ABCD中,P为对角线BD上任意一点,连接PA、PC,得到△PAB、△PBC、△PCD、△PDA,设它们的面积分别是S1、S2、S3、S4 , 给出如下结论:①S1=S2;②S1+S2=S3;③S1+S3=S2+S4;④若S1S3=S2S4 , 其中正确结论的序号是 . (在横线上填上你认为所有正确答案的序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠1=∠2,要使△ABD≌△ACD,需从下列条件中增加一个,错误的选法是( )
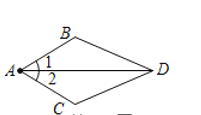
A.∠ADB=∠ADCB.∠B=∠CC.AB=ACD.DB=DC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AC∥DF,C、E分别在AB、DF上,小华想知道∠ACE和∠DEC是否互补,但是他有没有带量角器,只带了一副三角板,于是他想了这样一个办法:首先连结CF,再找出CF的中点O,然后连结EO并延长EO和直线AB相交于点B,经过测量,他发现EO=BO,因此他得出结论:∠ACE和∠DEC互补,而且他还发现BC=EF.

以下是他的想法,请你填上根据.小华是这样想的:
因为CF和BE相交于点O,
根据 得出∠COB=∠EOF;
而O是CF的中点,那么CO=FO,又已知 EO=BO,
根据 得出△COB≌△FOE,
根据 得出BC=EF,
根据 得出∠BCO=∠F,
既然∠BCO=∠F,根据 出AB∥DF,
既然AB∥DF,根据 得出∠ACE和∠DEC互补.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,小明在自家楼顶上的点A处测量建在与小明家楼房同一水平线上邻居的电梯的高度,测得电梯楼顶部B处的仰角为45°,底部C处的俯角为26°,已知小明家楼房的高度AD=15米,求电梯楼的高度BC(结果精确到0.1米)(参考数据:sin26°≈0.44,cos26°≈0.90,tan26°≈0.49)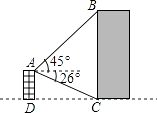
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个安装有进出水管的30升容器,水管单位时间内进出的水量是一定的,设从某时刻开始的4分钟内只进水不出水,在随后的8分钟内既进水又出水,得到水量y(升)与时间x(分)之间的函数关系如图所示.根据图象信思给出下列说法,其中错误的是( )

A. 每分钟进水5升
B. 每分钟放水1.25升
C. 若12分钟后只放水,不进水,还要8分钟可以把水放完
D. 若从一开始进出水管同时打开需要24分钟可以将容器灌满
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com