
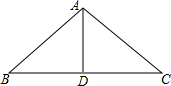
 如图,AB=AC,∠B=40°,点D在BC上,且∠DAC=50°.求证:BD=CD.
如图,AB=AC,∠B=40°,点D在BC上,且∠DAC=50°.求证:BD=CD. 科目:初中数学 来源: 题型:解答题
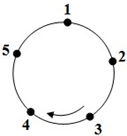 如图,圆上有五个点,这五个点将圆分成五等份(每一份称为一段弧长),把这五个点按顺时针方向依次编号为1,2,3,4,5,若从某一点开始,沿圆周顺时针方向行走,点的编号是数字几,就走几段弧长,则称这种走法为一次“移位”.如:小明在编号为3的点,那么他应走3段弧长,即从3→4→5→1为第一次“移位”,这时他到达编号为1的点,然后从1→2为第二次“移位”.
如图,圆上有五个点,这五个点将圆分成五等份(每一份称为一段弧长),把这五个点按顺时针方向依次编号为1,2,3,4,5,若从某一点开始,沿圆周顺时针方向行走,点的编号是数字几,就走几段弧长,则称这种走法为一次“移位”.如:小明在编号为3的点,那么他应走3段弧长,即从3→4→5→1为第一次“移位”,这时他到达编号为1的点,然后从1→2为第二次“移位”.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
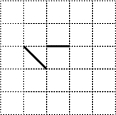 在如图的正方形网格上画有两条线段.现在要再画一条,使图中的三条线段组成一个轴对称图形,能满足条件的线段有( )
在如图的正方形网格上画有两条线段.现在要再画一条,使图中的三条线段组成一个轴对称图形,能满足条件的线段有( )| A. | 2条 | B. | 3条 | C. | 4条 | D. | 5条 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知线段OA的端点O在原地,∠1=30°,OA=2,在数轴上找一点P,使得△AOP是等腰三角形,并求出点P所表示的数,如果将∠1=30°改为45°或60°,那么点P所表示的数又是多少?
如图,已知线段OA的端点O在原地,∠1=30°,OA=2,在数轴上找一点P,使得△AOP是等腰三角形,并求出点P所表示的数,如果将∠1=30°改为45°或60°,那么点P所表示的数又是多少?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,圆柱形油槽内原有积油的水平面宽CD=60cm,油深为10cm.若油面上升10cm,则此时油面宽AB为多少?(教材124页第10题改编)
如图,圆柱形油槽内原有积油的水平面宽CD=60cm,油深为10cm.若油面上升10cm,则此时油面宽AB为多少?(教材124页第10题改编)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com