
 城市规划期间,欲拆除一电线杆AB,如图,已知大坝背水坡ED的坡角∠EDG=60°,背水坡ED的垂直高度EH为6米,在坝顶E处有一高为1米的测角仪EF,测得杆顶A的仰角为20°,杆底B的俯角为20°,C、D之间是2米宽的人行道,在拆除电线杆AB时,为确保行人安全,是否需要将此人行道封闭?请说明理由(在地面上,以点B为圆心,以AB为半径的圆形区域为危险区域).(tan20°≈0.4,tan70°≈2.7,$\sqrt{3}$≈1.7)
城市规划期间,欲拆除一电线杆AB,如图,已知大坝背水坡ED的坡角∠EDG=60°,背水坡ED的垂直高度EH为6米,在坝顶E处有一高为1米的测角仪EF,测得杆顶A的仰角为20°,杆底B的俯角为20°,C、D之间是2米宽的人行道,在拆除电线杆AB时,为确保行人安全,是否需要将此人行道封闭?请说明理由(在地面上,以点B为圆心,以AB为半径的圆形区域为危险区域).(tan20°≈0.4,tan70°≈2.7,$\sqrt{3}$≈1.7) 分析 先根据直角三角形的性质求出DH的长,再过点F作FM⊥AB,垂足为M,由∠AFM=∠BFM=20°可知AF=BF,故AM=BM.根据矩形的判定定理得出四边形FHBM是矩形,故可得出BM=FH=7,据此可得出AB的长,再由直角三角形的性质得出BH的长,进而得出BC的长,再与AB的长相比较即可.
解答  解:需要将此人行道封闭.
解:需要将此人行道封闭.
理由:∵∠EDH=60°,EH=6,
∴DH=$\frac{EH}{tan60°}$=$\frac{6}{\sqrt{3}}$=2$\sqrt{3}$.
过点F作FM⊥AB,垂足为M,
∵∠AFM=∠BFM=20°,
∴AF=BF,
∴AM=BM.
∵FH⊥BG,FM⊥AB,AB⊥BG,
∴四边形FHBM是矩形,
∴BM=FH=7,∠HBF=∠BFM=20°,
∵EF=1,
∴FH=EH+EF=6+1=7,
∴AB=14,BH=$\frac{FH}{tan20°}$=$\frac{6+1}{0.4}$≈17.5,
∴BC=BH-DH-CD=17.5-2$\sqrt{3}$-2≈17.5-3.4-2=12.1<14,
∴需要将此人行道封闭.
点评 本题考查的是解直角三角形的应用-仰角俯角问题,熟记锐角三角函数的定义是解答此题的关键.


 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | AC=BD | B. | AC⊥BD | C. | ∠ABD=∠BAC | D. | ∠BAC+∠CAD=90° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
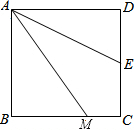 如图,已知四边形ABCD是正方形,M是BC边上一点,E是CD边的中点,AE平分∠DAM.
如图,已知四边形ABCD是正方形,M是BC边上一点,E是CD边的中点,AE平分∠DAM.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com