
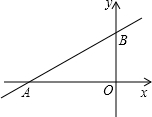
 如图,一次函数y=kx+b图象经过点A(-4,0)和点B(0,2),
如图,一次函数y=kx+b图象经过点A(-4,0)和点B(0,2),分析 (1)将点A、B坐标代入一次函数y=kx+b求出k、b即可;
(2)设点P的纵坐标为(m,n),根据△AOP的面积为2列出关于n的方程,解方程可得n的值,将n代回解析式可得坐标.
解答 解:(1)设一次函数解析式为:y=kx+b,
根据题意,将点A(-4,0)和点B(0,2)代入得:
$\left\{\begin{array}{l}{-4k+b=0}\\{b=2}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=\frac{1}{2}}\\{b=2}\end{array}\right.$,
∴一次函数解析式为:y=$\frac{1}{2}$x+2;
(2)设点P的纵坐标为(m,n),
∵OA=4,且△AOP的面积为1,
∴$\frac{1}{2}$×4×|n|=1,
解得:n=$\frac{1}{2}$或n=-$\frac{1}{2}$,
当n=$\frac{1}{2}$时,有$\frac{1}{2}$m+2=$\frac{1}{2}$,解得:m=-3,∴点P(-3,$\frac{1}{2}$);
当n=-$\frac{1}{2}$时,由$\frac{1}{2}$m+2=-$\frac{1}{2}$,解得:m=-5,∴点P(-5,-$\frac{1}{2}$);
综上,点P的坐标为:(-3,$\frac{1}{2}$)或(-5,-$\frac{1}{2}$).
点评 本题考查的是一次函数图象上点的坐标特点,熟知一次函数图象上各点的坐标一定适合此函数的解析式是解答此题的关键.


 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案科目:初中数学 来源: 题型:填空题
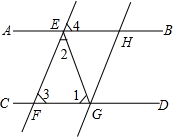 如图所示,下列结论正确的有①③④(把所有正确结论的序号都选上)
如图所示,下列结论正确的有①③④(把所有正确结论的序号都选上)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
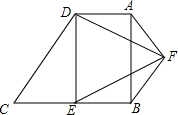 如图,在四边形ABCD中,AD∥BC,∠ABC=90°,∠C=60°,E是BC的中点,BC=2AD=$2\sqrt{3}$,△DEF是等边三角形,连结BF、AF.
如图,在四边形ABCD中,AD∥BC,∠ABC=90°,∠C=60°,E是BC的中点,BC=2AD=$2\sqrt{3}$,△DEF是等边三角形,连结BF、AF.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
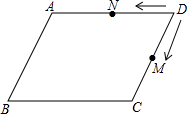 如图,?ABCD中,AB=4cm,BC=8cm,动点M从点D出发,按折线DCBAD方向以2cm/s的速度运动,动点N从点D出发,按折线DABCD方向以1cm/s的速度运动,两点均运动到点D停止.
如图,?ABCD中,AB=4cm,BC=8cm,动点M从点D出发,按折线DCBAD方向以2cm/s的速度运动,动点N从点D出发,按折线DABCD方向以1cm/s的速度运动,两点均运动到点D停止.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{9}$ | B. | $\sqrt{20}$ | C. | $\sqrt{\frac{1}{3}}$ | D. | $\sqrt{7}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com