
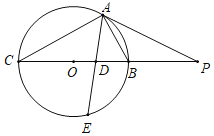
【题目】如图,△ABC内接于⊙O,BC为直径,∠BAC的平分线与BC和⊙O分别相交于D和E,P为CB延长线上一点,PB=5,PA=10,且∠DAP=∠ADP.
(1)求证:PA与⊙O相切;
(2)求sin∠BAP的值;
(3)求ADAE的值.
【答案】(1)详见解析;(2)![]() ;(3)90.
;(3)90.
【解析】
(1)连接OA,由三角形的外角性质和角平分线得出∠PAB=∠C,由等腰三角形的性质得出∠OAC=∠C=∠PAB,由圆周角定理得出∠BAC=90°,证出∠OAP=90°,即AP⊥OA,即可得出PA与⊙O相切;
(2)证明△PAB∽△PCA,得出![]() 得出
得出![]() ,即可得出结果;
,即可得出结果;
(3)连接CE,由切割线定理求出PC=20,得出BC=PC﹣PB=15,求出![]()
![]() ,再证明△ACE∽△ADB,得出
,再证明△ACE∽△ADB,得出![]() ,即可得出结果.
,即可得出结果.
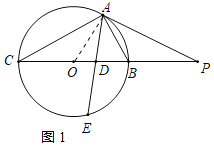
(1)证明:连接OA,如图1所示:
∵AE平分∠BAC,
∴∠BAD=∠CAD,
∵∠DAP=∠BAD+∠PAB,∠ADP=∠CAD+∠C,∠DAP=∠ADP,
∴∠PAB=∠C,
∵OA=OC,
∴∠OAC=∠C=∠PAB,
∵BC为直径,
∴∠BAC=90°,即∠OAC+∠OAB=90°,
∴∠PAB+∠OAB=90°,即∠OAP=90°,
∴AP⊥OA,
∴PA与⊙O相切;
(2)解:∵∠P=∠P,∠PAB=∠C,
∴△PAB∽△PCA,
∴![]()
∵∠CAB=90°,
∴![]()
∴sin∠BAP=sin∠C=![]() ;
;
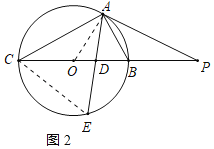
(3)解:连接CE,如图2所示:
∵PA与⊙O相切,
∴PA2=PB×PC,即102=5×PC,
∴PC=20,
∴BC=PC﹣PB=15,
∵![]()
∴![]()
![]() ,
,
∵AE是∠BAC的角平分线,
∴∠BAD=∠CAE,
∵∠E=∠ABD,
∴△ACE∽△ADB,
∴![]()
∴![]()


科目:初中数学 来源: 题型:
【题目】(2016山西省)我省某苹果基地销售优质苹果,该基地对需要送货且购买量在2000kg﹣5000kg(含2000kg和5000kg)的客户有两种销售方案(客户只能选择其中一种方案):
方案A:每千克5.8元,由基地免费送货.
方案B:每千克5元,客户需支付运费2000元.
(1)请分别写出按方案A,方案B购买这种苹果的应付款y(元)与购买量x(kg)之间的函数表达式;
(2)求购买量x在什么范围时,选用方案A比方案B付款少;
(3)某水果批发商计划用20000元,选用这两种方案中的一种,购买尽可能多的这种苹果,请直接写出他应选择哪种方案.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,抛物线
中,抛物线![]() (
(![]() )与
)与![]() 轴交于
轴交于![]() 、
、![]() 两点(点
两点(点![]() 在点
在点![]() 左侧),与
左侧),与![]() 轴交于点
轴交于点![]() ,该抛物线的顶点
,该抛物线的顶点![]() 的纵坐标是
的纵坐标是![]() .
.

(1)求点![]() 、
、![]() 的坐标;
的坐标;
(2)设直线与直线![]() 关于该抛物线的对称轴对称,求直线的表达式;
关于该抛物线的对称轴对称,求直线的表达式;
(3)平行于![]() 轴的直线
轴的直线![]() 与抛物线交于点
与抛物线交于点![]() 、
、![]() ,与直线交于点
,与直线交于点![]() .若
.若![]() ,结合函数图象,求
,结合函数图象,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
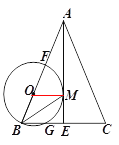
【题目】如图,在△ABC中,AB=AC,AE是BC边上的高线,BM平分∠ABC交AE于点M,经过B,M 两点的⊙O交BC于点G,交AB于点F ,FB为⊙O的直径.
(1)求证:AM是⊙O的切线
(2)当BE=3,cosC=![]() 时,求⊙O的半径.
时,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
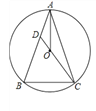
【题目】如图,△ABC内接于⊙O,AB=AC,CO的延长线交AB于点D.
(1)求证:AO平分∠BAC;
(2)若BC=6,sin∠BAC=![]() ,求AC和CD的长.
,求AC和CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
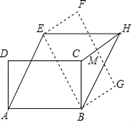
【题目】如图,矩形ABCD中,AB=3,AD=![]() ,将矩形ABCD绕点B按顺时针方向旋转后得到矩形EBGF,此时恰好四边形AEHB为菱形,连接CH交FG于点M,则HM=( )
,将矩形ABCD绕点B按顺时针方向旋转后得到矩形EBGF,此时恰好四边形AEHB为菱形,连接CH交FG于点M,则HM=( )
A. ![]() B. 1 C.
B. 1 C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,AB是⊙O的直径,AB=4,点F,C是⊙O上两点,连接AC,AF,OC,弦AC平分∠FAB,∠BOC=60°,过点C作CD⊥AF交AF的延长线于点D,垂足为点D.
(1)求扇形OBC的面积(结果保留π);
(2)求证:CD是⊙O的切线.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com