
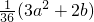
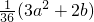 ,二次项系数3决定抛物线的开口方向和大小,所以a取任何不同的数值时,对应的抛物线的形状完全相同.
,二次项系数3决定抛物线的开口方向和大小,所以a取任何不同的数值时,对应的抛物线的形状完全相同. (12+2b),顶点坐标为(
(12+2b),顶点坐标为( ,
, b);
b); (27+2b),顶点坐标为(-
(27+2b),顶点坐标为(- ,
, b);
b);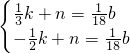 ,
,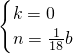 .
. b.
b.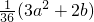 的顶点坐标为(-
的顶点坐标为(- ,
, b),
b), b,
b, b上.
b上.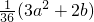 ,二次项系数3决定抛物线的开口方向和大小,即可判断对错.
,二次项系数3决定抛物线的开口方向和大小,即可判断对错. b是常数函数,此知识点初中教材不要求掌握,因此本题属于竞赛题型,有一定难度.
b是常数函数,此知识点初中教材不要求掌握,因此本题属于竞赛题型,有一定难度. 

科目:初中数学 来源: 题型:
| 3 |
| 3 |
| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| 1 | 36 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 m(m>O)与x轴交于点D.
m(m>O)与x轴交于点D.查看答案和解析>>
科目:初中数学 来源:2006年浙江省宁波市第七届特级教师跨区域带徒考核笔试卷(解析版) 题型:解答题
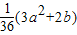
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com