
【题目】小华同学对图形旋转前后的线段之间、角之间的关系进行了拓展探究.
(一)猜测探究
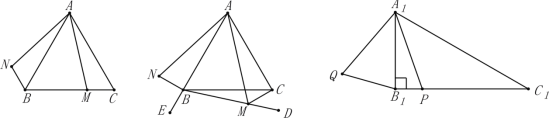
在△ABC中,AB=AC,M是平面内任意一点,将线段AM绕点A按顺时针方向旋转与∠BAC相等的角度,得到线段AN,连接NB.
(1)如图1,若M是线段BC上的任意一点,请直接写出∠NAB与∠MAC的数量关系是_______,NB与MC的数量关系是_______;
(2)如图2,点E是AB延长线上点,若M是∠CBE内部射线BD上任意一点,连接MC,(1)中结论是否仍然成立?若成立,请给予证明,若不成立,请说明理由。
(二)拓展应用
如图3,在△A1B1C1中,A1B1=8,∠A1B1C1=90°,∠C1=30°,P是B1C1上的任意点,连接A1P,将A1P绕点A1按顺时针方向旅转60°,得到线段A1Q,连接B1Q.求线段B1Q长度的最小值.
【答案】(一)(1)∠NAB=∠MAC,BN=MC;(2)成立,理由见解析;(二)QB1的最小值为4![]() -4
-4![]()
【解析】
(一)(1)由旋转知,AM=AN,∠BAC=∠NAM,进而得出∠MAC=∠NAB,判断出△CAM≌△BAN,即可得出结论;
(2)由旋转知,AM=AN,∠BAC=∠NAM,进而得出∠MAC=∠NAB,判断出△CAM≌△BAN,即可得出结论;
(二)如图3中,在A1 C1上截取A1N= A1 B1,连接PN,作NH⊥B1C1于H,作A1M⊥B1C1于M.理由全等三角形的性质证明B1Q=PN,推出当PN的值最小时,Q B1的值最小,求出HN的值即可解决问题.
解:(一)(1)结论:∠NAB=∠MAC,BN=MC.
理由:如图1中,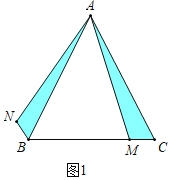
∵∠MAN=∠CAB,
∴∠NAB+∠BAM=∠BAM+∠MAC,
∴∠NAB=∠MAC,
∵AB=AC,AN=AM,
∴△NAB≌△MAC(SAS),
∴BN=CM.
故答案为:∠NAB=∠MAC,BN=CM,
(2)(1)中结论仍然成立,
理由:由旋转知,AM=AN,∠BAC=∠NAM,
∴∠BAC-∠BAM=∠NAM-∠BAM,
即:∠MAC=∠NAB,
∵AB=AC,
∴△CAM≌△BAN(SAS),
∴MC=NB;
(二)如图3中,在A1 C1上截取A1N= A1 B1,连接PN,作NH⊥B1 C1于H,作A1M⊥B1C1于M.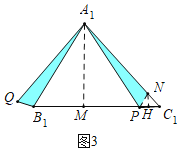
∵∠C1A B1=∠P A1Q,
∴∠Q A1 B1=∠P A1 N,
∵A1A= A1P,A1 B1=AN,
∴△Q A1 B1≌△P A1N(SAS),
∴B1Q=PN,
∴当PN的值最小时,Q B1的值最小,
在Rt△A1 B1M中,∵∠A1 B1M=60°,A1 B1=8,
∴A1M= A1 B1sin60°=4![]() ,
,
∵∠M A1 C1=∠B1 A1 C1-∠B1 A1M=75°-30°=45°,
∴A1 C1=4![]() ,
,
∴N C1= A1 C1- A1N=4![]() -8,
-8,
在Rt△NH C1,∵∠C1=45°,
∴NH=4![]() -4
-4![]() ,
,
根据垂线段最短可知,当点P与H重合时,PN的值最小,
∴Q B1的最小值为4![]() -4
-4![]()


科目:初中数学 来源: 题型:
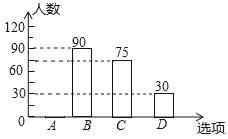
【题目】某校决定在4月7日开展“世界无烟日”宣传活动,活动有A社区板报、B集会演讲、C喇叭广播、D发宣传画四种宣传方式.学校围绕“你最喜欢的宣传方式是什么?”,在全校学生中进行随机抽样调查四个选项中必选且只选一项,根据调查统计结果,绘制了两种不完整的统计图表.
选项 | 方式 | 百分比 |
A | 社区板报 | m |
B | 集会演讲 | 30% |
C | 喇叭广播 | 25% |
D | 发宣传画 | 10% |
请结合统计图表,回答下列问题:
(1)本次抽查的学生共 人,m= ,并将条形统计图补充完整;
(2)若该校学生有900人,请你估计该校喜欢“集会演讲”这项宣传方式的学生约有多少人?
(3)学校采用抽签方式让每班在A、B、C、D四种宣传方式中随机抽取两种进行展示.请用树状图或列表法求某班所抽到的两种方式恰好是“集会演讲”和“喇叭广播”的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明想了解全校3000名同学对新闻、体育、音乐、娱乐、戏曲五类电视节目的喜爱况,从中抽取了一部分同学进行了一次抽样调查,利用所得数据绘制成下面的统计图:根据图中所给信息,全校喜欢娱乐类节目的学生大约有( )人.
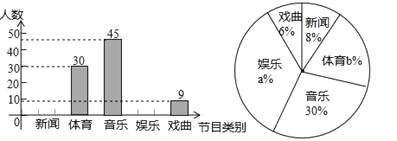
A. 1080 B. 900 C. 600 D. 108
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小张骑自行车匀速从甲地到乙地,在途中因故停留了一段时间后,仍按原速骑行,小李骑摩托车比小张晚出发一段时间,以800米/分的速度匀速从乙地到甲地,两人距离乙地的路程y(米)与小张出发后的时间x(分)之间的函数图象如图所示.
(1)求小张骑自行车的速度;
(2)求小张停留后再出发时y与x之间的函数表达式;
(3)求小张与小李相遇时x的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某日,正在我国南海海域作业的一艘大型渔船突然发生险情,相关部门接到求救信号后,立即调遣一架直升飞机和一艘刚在南海巡航的渔政船前往救援.当飞机到达距离海面3000米的高空C处,测得A处渔政船的俯角为60°,测得B处发生险情渔船的俯角为30°,请问:此时渔政船和渔船相距多远?(结果保留根号)
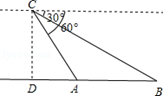
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 在正方形ABCD中.
(1)如图1,点E、F分别在BC、CD上,AE、BF相交于点O,∠AOB=90°,试判断AE与BF的数量关系,并说明理由;
(2)如图2,点E、F、G、H分别在边BC、CD、DA、AB上,EG、FH相交于点O,∠GOH=90°,且EG=7,求FH的长;
(3)如图3,点E、F分别在BC、CD上,AE、BF相交于点O,∠AOB=90°,若AB=5,图中阴影部分的面积与正方形的面积之比为4:5,求△ABO的周长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在一面靠墙(墙的最大可用长度为8 m)的空地上用长为24 m的篱笆围成中间隔有二道篱笆的长方形花圃.设花圃的宽AB为x m,面积为S m2.
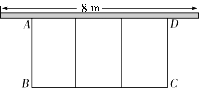
(1)求S关于x的函数关系式及自变量的取值范围;
(2)求所围成花圃的最大面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】4件同型号的产品中,有1件不合格品和3件合格品.
(1)从这4件产品中随机抽取1件进行检测,求抽到的是不合格品的概率;
(2)从这4件产品中随机抽取2件进行检测,求抽到的都是合格品的概率;
(3)在这4件产品中加入x件合格品后,进行如下试验:随机抽取1件进行检测,然后放回,多次重复这个试验,通过大量重复试验后发现,抽到合格品的频率稳定在0.95,则可以推算出x的值大约是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com