
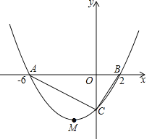
【题目】如图所示,抛物线![]() 的顶点为
的顶点为![]() ,与
,与![]() 轴交于
轴交于![]() 、
、![]() 两点,且
两点,且![]() ,与
,与![]() 轴交于点
轴交于点![]() .
.
![]() 求抛物线的函数解析式;
求抛物线的函数解析式;
![]() 求
求![]() 的面积;
的面积;
![]() 能否在抛物线第三象限的图象上找到一点
能否在抛物线第三象限的图象上找到一点![]() ,使
,使![]() 的面积最大?若能,请求出点
的面积最大?若能,请求出点![]() 的坐标;若不能,请说明理由.
的坐标;若不能,请说明理由.
科目:初中数学 来源: 题型:
【题目】如图,在边长为1的小正方形组成的网格中,△ABC的顶点均在格点上,请按要求完成下列各题:
(1)以原点O为对称中心作△ABC的中心对称图形,得到△A1B1C1,请画出△A1B1C1,并直接写出A1、B1、C1的坐标;
(2)再将△A1B1C1绕着点A1顺时针旋转90°,得到△A1B2C2,请画出△A1B2C2,并直接写出点B2、C2的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,![]() ,边
,边![]() 、
、![]() 都在
都在![]() 轴的正半轴上,
轴的正半轴上,![]() ,
,![]() ,
,![]() ,
,![]() .反比例函数
.反比例函数![]() 的图象经过点
的图象经过点![]() ,交
,交![]() 边于点
边于点![]() ,交
,交![]() 边于点
边于点![]() .
.

(1)分别求出点![]() 、
、![]() 的坐标;
的坐标;
(2)求以![]() 、
、![]() 、
、![]() 为顶点的
为顶点的![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() 的图象如图所示,则下列结论:其中正确的有( )
的图象如图所示,则下列结论:其中正确的有( )
①![]() ;
;![]() ;②方程
;②方程![]() 有两个不等的实数根;③
有两个不等的实数根;③![]() 随
随![]() 的增大而增大;④
的增大而增大;④![]() .
.
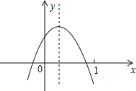
A. ![]() 个 B.
个 B. ![]() 个 C.
个 C. ![]() 个 D.
个 D. ![]() 个
个
查看答案和解析>>
科目:初中数学 来源: 题型:
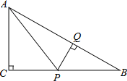
【题目】在![]() 中,
中,![]() ,
,![]() 是
是![]() 边上不同于
边上不同于![]() 、
、![]() 的一动点,过
的一动点,过![]() 作
作![]() ,垂足为
,垂足为![]() ,连接
,连接![]() .
.
![]() 试说明不论点
试说明不论点![]() 在
在![]() 边上何处时,都有
边上何处时,都有![]() 与
与![]() 相似;
相似;
![]() 若
若![]() ,
,![]() ,当
,当![]() 为何值时,
为何值时,![]() 面积最大,并求出最大值;
面积最大,并求出最大值;
![]() 在
在![]() 中,两条直角边
中,两条直角边![]() 、
、![]() 满足关系式
满足关系式![]() ,是否存在一个
,是否存在一个![]() 的值,使
的值,使![]() 既与
既与![]() 全等,也与
全等,也与![]() 全等.
全等.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,BD为一条对角线,AD∥BC,AD=2BC,∠ABD=90°,E为AD的中点,连接BE.
(1)求证:四边形BCDE为菱形;
(2)连接AC,若AC平分∠BAD,BC=1,求AC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题提出:
(1)如图①,若正方形![]() 的边长为6,点
的边长为6,点![]() 分别为边
分别为边![]() 上的点,且
上的点,且![]() ,
,![]() 与
与![]() 交于点
交于点![]() ,连接
,连接![]() ,则
,则![]() ;
;
问题探究:
(2)如图②,![]() ,
,![]() 是等腰直角三角形,顶点
是等腰直角三角形,顶点![]() 分别在
分别在![]() 的两边上,试说明点
的两边上,试说明点![]() 在
在![]() 的平分线上;
的平分线上;
问题解决:
(3)如图③,![]() ,
,![]() 是等边三角形,顶点
是等边三角形,顶点![]() 分别在
分别在![]() 的两边上,点
的两边上,点![]() 在
在![]() 上,且
上,且![]() ,连接
,连接![]() ,求
,求![]() 的最小值.
的最小值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了了解初一年级学生每学期参加综合实践活动的情况,某区教育行政部门随机抽样调查了部分初一学生一个学期参加综合实践活动的天数,并用得到的数据绘制了统计图①和图②,请根据图中提供的信息,回答下列问题:
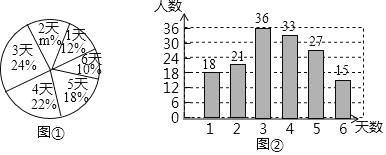
(I)本次随机抽样调查的学生人数为 ,图①中的m的值为 ;
(II)求本次抽样调查获取的样本数据的众数、中位数和平均数;
(III)若该区初一年级共有学生2500人,请估计该区初一年级这个学期参加综合实践活动的天数大于4天的学生人数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com