
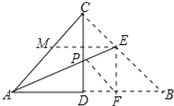
【题目】如图,将一个等腰Rt△ABC对折,使∠A与∠B重合,展开后得折痕CD,再将∠A折叠,使C落在AB上的点F处,展开后,折痕AE交CD于点P,连接PF、EF,下列结论:①tan∠CAE=![]() ﹣1;②图中共有4对全等三角形;③若将△PEF沿PF翻折,则点E一定落在AB上;④PC=EC;⑤S四边形DFEP=S△APF.正确的个数是( )
﹣1;②图中共有4对全等三角形;③若将△PEF沿PF翻折,则点E一定落在AB上;④PC=EC;⑤S四边形DFEP=S△APF.正确的个数是( )

A. 1个 B. 2个 C. 3个 D. 4个
【答案】C
【解析】试题解析:①正确.作EM∥AB交AC于M.
∵CA=CB,∠ACB=90°,
∴∠CAB=∠CBA=45°,
∵∠CAE=∠BAE=![]() ∠CAB=22.5°,
∠CAB=22.5°,
∴∠MEA=∠EAB=22.5°,
∴∠CME=45°=∠CEM,设CM=CE=a,则ME=AM=![]() a,
a,
∴tan∠CAE=![]() ,故①正确,
,故①正确,
②正确.△CDA≌△CDB,△AEC≌△AEF,△APC≌△APF,△PEC≌△PEF,故②正确,
③正确.∵△PEC≌△PEF,
∴∠PCE=∠PFE=45°,
∵∠EFA=∠ACE=90°,
∴∠PFA=∠PFE=45°,
∴若将△PEF沿PF翻折,则点E一定落在AB上,故③正确.
④正确.∵∠CPE=∠CAE+∠ACP=67.5°,∠CEP=90°﹣∠CAE=67.5°,
∴∠CPE=∠CEP,
∴CP=CE,故④正确,
⑤错误.∵△APC≌△APF,
∴S△APC=S△APF,
假设S△APF=S四边形DFPE,则S△APC=S四边形DFPE,
∴S△ACD=S△AEF,
∵S△ACD=![]() S△ABC,S△AEF=S△AEC≠
S△ABC,S△AEF=S△AEC≠![]() S△ABC,
S△ABC,
∴矛盾,假设不成立.
故⑤错误.
 .
.
故选C.


 轻松暑假总复习系列答案
轻松暑假总复习系列答案科目:初中数学 来源: 题型:
【题目】问题发现:
(![]() )如图①,
)如图①,![]() 中,
中,![]() ,
,![]() ,
,![]() ,点
,点![]() 是
是![]() 边上任意一点,则
边上任意一点,则![]() 的最小值为__________.
的最小值为__________.
(![]() )如图②,矩形
)如图②,矩形![]() 中,
中,![]() ,
,![]() ,点
,点![]() 、点
、点![]() 分别在
分别在![]() 、
、![]() 上,求
上,求![]() 的最小值.
的最小值.
(![]() )如图③,矩形
)如图③,矩形![]() 中,
中,![]() ,
,![]() ,点
,点![]() 是
是![]() 边上一点,且
边上一点,且![]() ,点
,点![]() 是
是![]() 边上的任意一点,把
边上的任意一点,把![]() 沿
沿![]() 翻折,点
翻折,点![]() 的对应点为点
的对应点为点![]() ,连接
,连接![]() 、
、![]() ,四边形
,四边形![]() 的面积是否存在最小值,若存在,求这个最小值及此时
的面积是否存在最小值,若存在,求这个最小值及此时![]() 的长度;若不存在,请说明理由.
的长度;若不存在,请说明理由.



查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某人购进一批苹果到市场上零售,已知卖出苹果数量x与售价y的关系如下表.
数量x(千克) | 1 | 2 | 3 | 4 | 5 |
售价y(元) | 3+0.1 | 6+0.2 | 9+0.3 | 12+0.4 | 15+0.5 |
则当卖出苹果数量为10千克时,售价y为_______元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,△AOB的顶点O在直线l上,且AO=AB.

(1)画出△AOB关于直线l成轴对称的图形△COD,且使点A的对称点为点C ;
(2)在(1)的条件下,AC与BD的位置关系是________;
(3)在(1)、(2)的条件下,联结AD,如果∠ABD=2∠ADB,求∠AOC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=4,AD=6,点F是AB的中点,E为BC边上一点,且EF⊥ED,连结DF,M为DF的中点,连结MA,ME.若AM⊥ME,则AE的长为( )
A.5
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠MON=30°,B为OM上一点,BA⊥ON于A,四边形ABCD为正方形,P为射线BM上一动点,连结CP,将CP绕点C顺时针方向旋转90°得CE,连结BE,若AB=4,则BE的最小值为 . 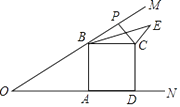
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校为了丰富学生课余生活,决定开设以下体育课外活动项目:A.版画 B.保龄球C.航模 D.园艺种植,为了解学生最喜欢哪一种活动项目,随机抽取了部分学生进行调查,并将调查结果绘制成了两幅不完整的统计图,请回答下列问题:
(1)这次被调查的学生共有 人;
(2)请你将条形统计图(2)补充完整;
(3)在平时的保龄球项目训练中,甲、乙、丙、丁四人表现优秀,现决定从这四名同学中任选两名参加保龄球比赛,求恰好选中甲、乙两位同学的概率(用树状图或列表法解答)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com