
| | A种产品 | B种产品 |
| 成本(万元/件) | 2 | 5 |
| 利润(万元/件) | 1 | 3 |
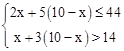 ,解得:2≤x<8。
,解得:2≤x<8。

 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 :
: 与直线
与直线 :
: 相交于点
相交于点 ,直线
,直线 与
与 轴交于点
轴交于点 ,平行于
,平行于 轴的直线
轴的直线 分别交直线
分别交直线 、直线
、直线 于
于 、
、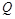 两点(点
两点(点 在
在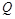 的左侧)
的左侧) 的坐标为 ;
的坐标为 ; 在线段
在线段 上,在
上,在 轴上是否存在一点
轴上是否存在一点 ,使得
,使得 为等腰直角三角形,若存在,求出点
为等腰直角三角形,若存在,求出点 的坐标;若不存在,说明理由;
的坐标;若不存在,说明理由; 为直角顶点,向下作等腰直角
为直角顶点,向下作等腰直角 ,设
,设 与
与 重叠部分的面积为
重叠部分的面积为 ,求
,求 与
与 的函数关系式;并注明
的函数关系式;并注明 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
| 每千克售价(元) | 38 | 37 | 36 | 35 | … | 20 |
| 每天销量(千克) | 50 | 52 | 54 | 56 | … | 86 |
 元时,销售量为
元时,销售量为 千克;
千克; 与
与 间的函数关系式(不用写出自变量的取值范围);
间的函数关系式(不用写出自变量的取值范围);查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题


查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题

| A.甲、乙两地的路程是400千米 |
| B.慢车行驶速度为60千米/小时 |
| C.相遇时快车行驶了150千米 |
| D.快车出发后4小时到达乙地 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com