
分析 利用因式分解的方法得到(a+3b)2+(a-1)2=0,再根据非负数的性质得到$\left\{\begin{array}{l}{a+3b=0}\\{a-1=0}\end{array}\right.$,求出a与b的值后代入a2b+3ab2,计算即可.
解答 解:∵2a2+6ab+9b2-2a+1=0,
∴(a+3b)2+(a-1)2=0,
∴$\left\{\begin{array}{l}{a+3b=0}\\{a-1=0}\end{array}\right.$,
∴$\left\{\begin{array}{l}{a=1}\\{b=-\frac{1}{3}}\end{array}\right.$,
∴a2b+3ab2
=ab(a+3b)
=ab×0
=0.
点评 本题考查了因式分解的应用及非负数的性质,属于基础题,关键是掌握几个非负数相加等于0,各个非负数都为0.


 快乐5加2金卷系列答案
快乐5加2金卷系列答案科目:初中数学 来源: 题型:选择题
| A. | m=-7,n=3 | B. | m=7,n=-3 | C. | m=-7,n=-3 | D. | m=7,n=3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
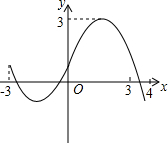 若y是关于x的函数,H是常数(H>0),若对于此函数图象上的任意两点(x1,y1),(x2,y2),都有|y1-y2|≤H,则称该函数为有界函数,其中满足条件的所有常数H的最小值,称为该函数的界高.如下图所表示的函数的界高为4.
若y是关于x的函数,H是常数(H>0),若对于此函数图象上的任意两点(x1,y1),(x2,y2),都有|y1-y2|≤H,则称该函数为有界函数,其中满足条件的所有常数H的最小值,称为该函数的界高.如下图所表示的函数的界高为4.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
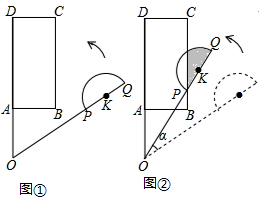 平面上,矩形ABCD与直径为QP的半圆K如图如图①摆放,分别延长DA和QP交于点O,且∠DOQ=60°,OQ=OD=3,OP=2,OA=AB=1.让线段OD及矩形ABCD位置固定,将线段OQ连带着半圆K一起绕着点O按逆时针开始旋转,如图②,当点P恰好落在BC边上时,S阴影=$\frac{π}{24}$+$\frac{\sqrt{3}}{16}$.
平面上,矩形ABCD与直径为QP的半圆K如图如图①摆放,分别延长DA和QP交于点O,且∠DOQ=60°,OQ=OD=3,OP=2,OA=AB=1.让线段OD及矩形ABCD位置固定,将线段OQ连带着半圆K一起绕着点O按逆时针开始旋转,如图②,当点P恰好落在BC边上时,S阴影=$\frac{π}{24}$+$\frac{\sqrt{3}}{16}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com