
【题目】某中学库存960套旧课桌椅准备修理。现有甲、乙两个木工小组都想承接这项业务。经协商后得知:甲小组单独修理这批桌椅比乙小组多用20天;乙小组每天比甲小组多修8套;学校每天需付甲小组修理费80元,付乙小组120元。
(1)求甲、乙两个小组每天各修理桌櫈多少套?
(2)在修理过程中,学校要委派一名修理工进行质量监督,并由学校负担他每天的生活补助10元,现有以下三种修理方案供选择:①由甲单独修理;②由乙单独修理;③由甲、乙共同合作修理。你认为哪种方案既省时又省钱?试比较说明。
【答案】(1)甲每天修理就课桌椅16套,乙每天修理课桌椅24套;(2)甲乙合作
【解析】试题分析:(1)设甲每天修理旧课桌椅x套,则乙每天修理旧课桌椅(x+8)套,根据甲小组单独修理这批桌椅比乙小组多用20天,即可列方程求解;
(2)分别计算出各种方案所需费用,再比较即可判断.
(1)设甲每天修理旧课桌椅x套,则乙每天修理旧课桌椅(x+8)套,由题意得
![]()
解得![]() (舍),
(舍),![]()
![]() (套)
(套)
答:甲每天修理旧课桌椅16套,乙每天修理旧课桌椅24套;
(2)甲单独完成需要960÷16=60天,需要![]() 元
元
乙单独完成需要960÷24=40天,需要![]() 元
元
甲乙合作需要960÷(16+24)=24天,需要![]() 元
元
所以选择甲乙合作完成。


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】著名的瑞士数学家欧拉曾指出:可以表示为四个整数平方之和的甲、乙两数相乘,其乘积仍然可以表示为四个整数平方之和,即 ![]()
![]() ,这就是著名的欧拉恒等式,有人称这样的数为“不变心的数”.实际上,上述结论可概括为:可以表示为两个整数平方之和的甲、乙两数相乘,其乘积仍然可以表示为两个整数平方之和.
,这就是著名的欧拉恒等式,有人称这样的数为“不变心的数”.实际上,上述结论可概括为:可以表示为两个整数平方之和的甲、乙两数相乘,其乘积仍然可以表示为两个整数平方之和.
【阅读思考】
在数学思想中,有种解题技巧称之为“无中生有”.例如问题:将代数式 ![]() 改成两个平方之差的形式.解:原式
改成两个平方之差的形式.解:原式 ![]() ﹒
﹒
(1)【动手一试】试将 ![]() 改成两个整数平方之和的形式. (12+52)(22+72)=;
改成两个整数平方之和的形式. (12+52)(22+72)=;
(2)【解决问题】请你灵活运用利用上述思想来解决“不变心的数”问题:将代数式 ![]() 改成两个整数平方之和的形式(其中a、b、c、d均为整数),并给出详细的推导过程﹒
改成两个整数平方之和的形式(其中a、b、c、d均为整数),并给出详细的推导过程﹒
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知m<n,有下列关于m、n的命题:①6m>6n;②-3m<-3n;③m-5<n-5;④2m+5>2n+5.其中,所有正确命题的序号是___.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,O为平行四边形ABCD的对角线AC的中点,过点O作一条直线分别与AB,CD交于点M,N,点E,F在直线MN上,且OE=OF.
(1)图中共有几对全等三角形,请把它们都写出来;
(2)求证:∠MAE=∠NCF.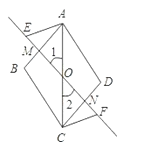
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com