
【题目】如图,在平面直角坐标系中,矩形OABC的顶点A、C的坐标分别为(9,0),(0,3),OD=5,点P在BC(不与点B、C重合)上运动,当△OPD为等腰三角形时,点P的坐标为______.

【答案】(1,3)或(4,3)或(2.5,3).
【解析】
根据当OP=OD时,以及当OD=PD时,OP=PD时分别进行讨论得出P点的坐标.
解:过P作PM⊥OA于M
当OP=OD时,如图1所示:
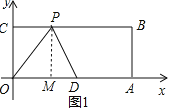
OP=5,CO=3,
由勾股定理得:CP=4,
∴P(4,3);
当OD=PD时如图2所示:
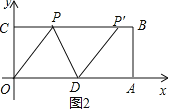
PD=DO=5,PM=3,
由勾股定理得:MD=4,
∴CP=5-4=1或CP'=9(不合题意).,
∴P(1,4);
当OP=PD时,根据等腰三角形三线合一的性质可知,点P的坐标为(2.5,3)
综上,满足题意的点P的坐标为(1,3)、(4,3)、(2.5,3).
故答案为:(1,3)或(4,3)、(2.5,3).


科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,D是BC的中点,DE⊥AB于E,DF⊥AC于F,BE=CF.

(1)∠B=70°,求∠CAD的大小;
(2)连接EF,求证:AD垂直平分EF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图在△ABC中,BF、CF是角平分线,DE∥BC,分别交AB、AC于点D、E,DE经过点F.结论:①△BDF和△CEF都是等腰三角形;②DE=BD+CE; ③△ADE的周长=AB+AC;④BF=CF.其中正确的是______.(填序号)

查看答案和解析>>
科目:初中数学 来源: 题型:
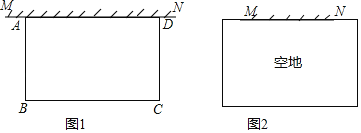
【题目】空地上有一段长为a米的旧墙MN,某人利用旧墙和木栏围成一个矩形菜园ABCD,已知木栏总长为100米.
(1)已知a=20,矩形菜园的一边靠墙,另三边一共用了100米木栏,且围成的矩形菜园面积为450平方米.如图1,求所利用旧墙AD的长;
(2)已知0<α<50,且空地足够大,如图2.请你合理利用旧墙及所给木栏设计一个方案,使得所围成的矩形菜园ABCD的面积最大,并求面积的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A. ![]() 一定是一次函数
一定是一次函数
B. 有的实数在数轴上找不到对应的点
C. 长为![]() 的三条线段能组成直角三角形
的三条线段能组成直角三角形
D. 无论![]() 为何值,点
为何值,点![]() 总是在第二象限
总是在第二象限
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将一矩形纸片OABC放在直角坐标系中,O为原点,C在x轴上,OA=6,OC=10.

(1)如图1,在OA上取一点E,将△EOC沿EC折叠,使O点落在AB边上的D点,求E点的坐标;
(2)如图2,在OA、OC边上选取适当的点E′、F,将△E′OF沿E′F折叠,使O点落在AB边上的D′点,过D′作D′G⊥C′O交E′F于T点,交OC′于G点,T坐标为(3,m),求m.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:线段AB,BC,![]() .
.
求作:矩形ABCD.

老师说甲、乙同学的作图都正确. 请你选择其中一位同学的作业说明其作图依据.
我选择____同学,他的作图依据是:___________________________________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一辆摩拜单车放在水平的地面上,车把头下方A处与坐垫下方B处在平行于地面的水平线上,A、B之间的距离约为49cm,现测得AC、BC与AB的夹角分别为45°与68°,若点C到地面的距离CD为28cm,坐垫中轴E处与点B的距离BE为4cm,求点E到地面的距离(结果保留一位小数).(参考数据:sin68°≈0.93,cos68°≈0.37,cot68°≈0.40)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在平面直角坐标系中,抛物线![]() 与x轴相交于点A,B,与y轴相交于点C,直线y=x+4经过A,C两点,
与x轴相交于点A,B,与y轴相交于点C,直线y=x+4经过A,C两点,
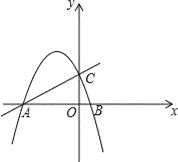
(1)求抛物线的表达式;
(2)如果点P,Q在抛物线上(P点在对称轴左边),且PQ∥AO,PQ=2AO,求P,Q的坐标;
(3)动点M在直线y=x+4上,且△ABC与△COM相似,求点M的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com