
分析 分类讨论:如图,当n>0时,作FM⊥y轴于M,AN⊥y轴于N,先证明△APN≌△PFM,得到AN=PM=1,PN=FM=n+1,则F(n+1,n-1),根据反比例函数图象上点的坐标特征有(n+1)(n-1)=8,解得n1=3,n2=-3(舍去),即n的值为3;当n<0时,四边形AP′F′G′为正方形,作F′G⊥y轴于Q,G′H⊥AN于H,如图,P′(0,n),同样方法可证明△ANP′≌△P′QF′≌△G′HA,则AN=P′Q=G′H=1,NP′=F′Q=AH=-1-n,所以F′(n+1,n-1),G′(n,-2),根据反比例函数图象上点的坐标特征(n+1)(n-1)=8或-2n=8,然后分别解方程求出对应n的值.
解答 解:如图,当n>0时,作FM⊥y轴于M,AN⊥y轴于N,
∵A(-1,-1),P(0,n),
∴AN=1,PN=n+1,
∵四边形APFG为正方形,
∴AP=FM,∠APF=90°,
即∠APN+∠FPM=90°,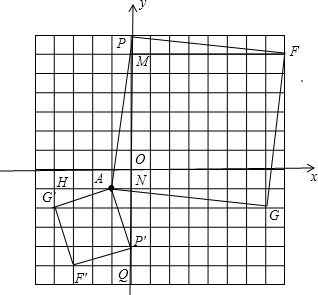
∵∠APN+∠PAN=90°,
∴∠PAN=∠FPM,
在△APN和△PFM中
$\left\{\begin{array}{l}{∠ANP=∠PMF}\\{∠PAN=FPM}\\{AP=PF}\end{array}\right.$,
∴△APN≌△PFM,
∴AN=PM=1,PN=FM=n+1,
∴F(n+1,n-1),
当F(n+1,n-1)在反比例函数y=$\frac{8}{x}$图象上,
∴(n+1)(n-1)=8,解得n1=3,n2=-3(舍去),即n的值为3;
当n<0时,四边形AP′F′G′为正方形,作F′G⊥y轴于Q,G′H⊥AN于H,如图,P′(0,n),
同样方法可证明△ANP′≌△P′QF′≌△G′HA,
∴AN=P′Q=G′H=1,NP′=F′Q=AH=-1-n,
∴F′(n+1,n-1),G′(n,-2),
当F′(n+1,n-1)在反比例函数y=$\frac{8}{x}$图象上,则(n+1)(n-1)=8,解得n1=-3,n2=3(舍去),即n的值为-3;
当G′(n,-2)在反比例函数y=$\frac{8}{x}$图象上,则-2n=8,解得n=-4,
综上所述,n的值为-3或-4或3.
故答案为-3或-4或3.
点评 本题考查了反比例函数图象上点的坐标特征:反比例函数y=$\frac{k}{x}$(k为常数,k≠0)的图象是双曲线,图象上的点(x,y)的横纵坐标的积是定值k,即xy=k.也考查了正方形的性质.本题的关键是根据题意画出几何图形.


 目标测试系列答案
目标测试系列答案科目:初中数学 来源: 题型:解答题
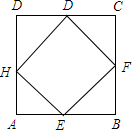 如图,长方形EFGH内接于边长为1的正方形ABCD,设AE=x,试求正方形EFGH的面积y与x的函数解析式,写出自变量x的取值范围,并求出AE=$\frac{1}{4}$时,正方形EFGH的面积.
如图,长方形EFGH内接于边长为1的正方形ABCD,设AE=x,试求正方形EFGH的面积y与x的函数解析式,写出自变量x的取值范围,并求出AE=$\frac{1}{4}$时,正方形EFGH的面积.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
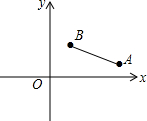 如图,在平面直角坐标系中,已知A(a,1),B(2,b),且a,b满足(2a-3b-2)2+$\sqrt{a-2b}$=0.
如图,在平面直角坐标系中,已知A(a,1),B(2,b),且a,b满足(2a-3b-2)2+$\sqrt{a-2b}$=0.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
| 已知:线段AB. 尺规作图:以线段AB为对角线作一个菱形ADBC. |
| 如图:(1)分别以A和B为圆心,大于$\frac{1}{2}$AB的长为半径画弧,两弧相交于C、D; (2)作四边形ADBC.  |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,已知A (4,2),B(2,-2),以点O为位似中心,按位似比1:2把△ABO缩小,则点A的对应点A′的坐标为(2,1)或(-2,-1).
如图,已知A (4,2),B(2,-2),以点O为位似中心,按位似比1:2把△ABO缩小,则点A的对应点A′的坐标为(2,1)或(-2,-1).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com