
【题目】已知:![]() ,OB、OM、ON,是
,OB、OM、ON,是![]() 内的射线.
内的射线.
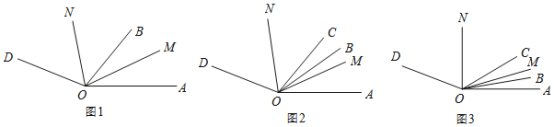
(1)如图 1,若 OM 平分 ![]() , ON平分
, ON平分![]() .当射线OB 绕点O 在
.当射线OB 绕点O 在![]() 内旋转时,
内旋转时,![]() = 度.
= 度.
(2)OC也是![]() 内的射线,如图2,若
内的射线,如图2,若![]() ,OM平分
,OM平分![]() ,ON平分
,ON平分![]() ,当射线OB绕点O在
,当射线OB绕点O在![]() 内旋转时,求
内旋转时,求![]() 的大小.
的大小.
(3)在(2)的条件下,当射线OB从边OA开始绕O点以每秒![]() 的速度逆时针旋转t秒,如图3,若
的速度逆时针旋转t秒,如图3,若![]() ,求t的值.
,求t的值.
【答案】(1)80;(2)70°;(3)26
【解析】
(1)根据角平分线的定义进行角的计算即可;
(2)依据OM平分∠AOC,ON平分∠BOD,即可得到∠MOC=![]() ∠AOC,∠BON=
∠AOC,∠BON=![]() ∠BOD,再根据∠MON=∠MOC+∠BON-∠BOC进行计算即可;
∠BOD,再根据∠MON=∠MOC+∠BON-∠BOC进行计算即可;
(3)依据∠AOM=![]() (10°+2t+20°),∠DON=
(10°+2t+20°),∠DON=![]() (160°-10°-2t),∠AOM:∠DON=2:3,即可得到3(30°+2t)=2(150°-2t),进而得出t的值.
(160°-10°-2t),∠AOM:∠DON=2:3,即可得到3(30°+2t)=2(150°-2t),进而得出t的值.
解:(1)∵∠AOD=160°,OM平分∠AOB,ON平分∠BOD,
∴∠MOB=![]() ∠AOB,∠BON=
∠AOB,∠BON=![]() ∠BOD,
∠BOD,
∴∠MON=∠MOB+∠BON=![]() ∠AOB+
∠AOB+![]() ∠BOD=
∠BOD=![]() (∠AOB+∠BOD)=
(∠AOB+∠BOD)=![]() ∠AOD=80°,
∠AOD=80°,
故答案为:80;
(2)∵OM平分∠AOC,ON平分∠BOD,
∴∠MOC=![]() ∠AOC,∠BON=
∠AOC,∠BON=![]() ∠BOD,
∠BOD,
∴∠MON=∠MOC+∠BON-∠BOC
=![]() ∠AOC+
∠AOC+![]() ∠BOD-∠BOC
∠BOD-∠BOC
=![]() (∠AOC+∠BOD)-∠BOC
(∠AOC+∠BOD)-∠BOC
=![]() ×180-20
×180-20
=70°;
(3)∵∠AOM=![]() (2t+20°),∠DON=
(2t+20°),∠DON=![]() (160°-2t),
(160°-2t),
又∠AOM:∠DON=2:3,
∴3(20°+2t)=2(160°-2t)
解得,t=26.
答:t为26秒.


 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案科目:初中数学 来源: 题型:
【题目】在抗洪抢险中,人民解放军的冲锋舟沿南北方向的河流抢救灾民.约定向北为正方向,某冲锋舟从 A 地出发,到达B地的一趟的航程记录如下(单位:千米):
![]()
(1)B地在A地的何方?相距多少千米?
(2)若冲锋舟每千米耗油![]() 升,油箱的容量为29 升,则途中至少需要补充多少升油?
升,油箱的容量为29 升,则途中至少需要补充多少升油?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为12,点E在边AB上,BE=8,过点E作EF∥BC,分别交BD、CD于G、F两点.若点P、Q分别为DG、CE的中点,则PQ的长为_____.
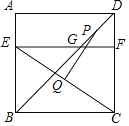
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解:
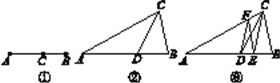
如图①,点C将线段AB分成两部分,若![]() ,则点C为线段AB的黄金分割点.
,则点C为线段AB的黄金分割点.
某研究学习小组,由黄金分割点联想到“黄金分割线”,从而给出“黄金分割线”的定义:直线l将一个面积为S的图形分成两部分,这两部分的面积分别为S1,S2,如果![]() ,那么称直线l为该图形的黄金分割线.
,那么称直线l为该图形的黄金分割线.
问题解决:
如图②,在△ABC中,已知D是AB的黄金分割点.
(1)研究小组猜想:直线CD是△ABC的黄金分割线,你认为对吗?为什么?
(2)请你说明:三角形的中线是否也是该三角形的黄金分割线?
(3)研究小组探究发现:过点C作直线交AB于点E,过点D作DF∥CE,交AC于点F,连接EF(如图③),则直线EF也是△ABC的黄金分割线.请你说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
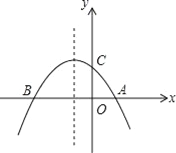
【题目】如图,已知抛物线y=﹣![]() x2﹣
x2﹣![]() x+2与x轴交于A、B两点,与y轴交于点C
x+2与x轴交于A、B两点,与y轴交于点C
(1)求点A,B,C的坐标;
(2)点E是此抛物线上的点,点F是其对称轴上的点,求以A,B,E,F为顶点的平行四边形的面积;
(3)此抛物线的对称轴上是否存在点M,使得△ACM是等腰三角形?若存在,请求出点M的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
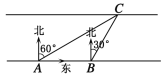
【题目】如图,甲、乙两人在道路的两边相向而行,当甲、乙两人分别行至点A、C时,测得乙在甲的北偏东60°方向上.乙留在原地休息,甲继续向前走了40米到B处,此时测得乙在其北偏东30°方向上.求道路的宽(参考数据:![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,已知 AD 是△ABC 的边 BC 上的中线.
(1)作出△ABD 的边 BD 上的高.
(2)若△ABC 的面积为 10,求△ADC 的面积.
(3)若△ABD 的面积为 6,且 BD 边上的高为 3,求 BC 的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题:已知α、β均为锐角,tanα=![]() ,tanβ=
,tanβ=![]() ,求α+β的度数.
,求α+β的度数.
探究:(1)用6个小正方形构造如图所示的网格图(每个小正方形的边长均为1),请借助这个网格图求出α+β的度数;
延伸:(2)设经过图中M、P、H三点的圆弧与AH交于R,求![]() 的弧长.
的弧长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com