
分析 (1)首先确定有关利润与售价x之间的二次函数,配方后即可确定最大利润;
(2)首先确定原来的销售量,然后根据销售量×售价=销售额列出方程求解即可.
解答 解:(1)∵销售量=250-10(x-25)=500-10x,
∴W=(x-20)(500-10x)
=-10x2+700x-10000
=-10(x-35)2+2250
∴当x=35时,最大利润为2250元.
(2)原来销售量500-10x=500-350=150,
35(1-m%)150(1+2m%)=5670
设m%=a,整理得:50a2-25a+2=0,
解得:a1=$\frac{2}{5}$,a2=$\frac{1}{10}$,
∵要使销量尽可能的大,
∴a=$\frac{2}{5}$=0.4
∴m=40.
点评 本题考查了列一元二次方程解实际问题的运用,一元二次方程的解法的运用,二次函数的性质的运用,解答时根据条件建立方程是解答本题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
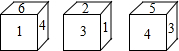 有一正方体,六个面上分别写有数字1、2、3、4、5、6,有三个人从不同的角度观察的结果如图所示.如果记1的对面的数字为a,3的对面的数字为b,那么a+b的值为( )
有一正方体,六个面上分别写有数字1、2、3、4、5、6,有三个人从不同的角度观察的结果如图所示.如果记1的对面的数字为a,3的对面的数字为b,那么a+b的值为( )| A. | 3 | B. | 7 | C. | 8 | D. | 11 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
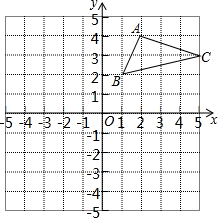 如图,在平面直角坐标系中,△ABC的三个顶点都在格点上,点A的坐标为(2,4),请解答下列问题:
如图,在平面直角坐标系中,△ABC的三个顶点都在格点上,点A的坐标为(2,4),请解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
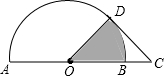 如图,AB为半圆O的直径,点C在AB的延长线上,CD与半圆O相切于点D,且AB=2CD=4,则图中阴影部分的面积为$\frac{π}{2}$.
如图,AB为半圆O的直径,点C在AB的延长线上,CD与半圆O相切于点D,且AB=2CD=4,则图中阴影部分的面积为$\frac{π}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
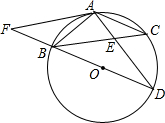 如图,在⊙O中,弦AB=AC,BD为⊙O的直径,AD交BC于E,AF∥BC交DB的延长线于点F,AE=2,ED=4.
如图,在⊙O中,弦AB=AC,BD为⊙O的直径,AD交BC于E,AF∥BC交DB的延长线于点F,AE=2,ED=4.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com