
【题目】对于实数a和b,定义新运算“@”:a@b=![]()
(1)计算20182018@(8@28)的值;
(2)若(x﹣1)@(3﹣2x)=2,求实数x的值;
(3)设函数y1=(2﹣x2)@(4x﹣x2),若函数y2=y1﹣m的图象与x轴恰有两个交点,求实数m的取值范围.
【答案】(1)20181982;(2)x=0或2;(3)m<6.
【解析】
(1)根据行定义即可求解,(2)分类讨论进行求解,(3)分类讨论,再根据函数y2=y1﹣m的图象与x轴恰有两个交点,即整理出的一元二次方程中的△>0,解不等式即可解题.
解:(1)20182018@(8@28)=20182018@(8+28)=20182018﹣36=20181982;
(2)①当x﹣1≤3﹣2x,即x≤![]() 时,(x﹣1)@(3﹣2x)=(x﹣1)+(3﹣2x)=2,解得:x=0;
时,(x﹣1)@(3﹣2x)=(x﹣1)+(3﹣2x)=2,解得:x=0;
②当x﹣1>3﹣2x,同理可得:x=2;
故x=0或2;
(3)①当(2﹣x2)≤(4x﹣x2),即x≥![]() ,
,
y2=y1﹣m=(2﹣x2)﹣(4x﹣x2)﹣m,
△=16﹣4×(﹣2)(2﹣m)>0,
解得:m<6;
②当(2﹣x2)>(4x﹣x2),
同理可得:y2=y1﹣m=(2﹣x2)﹣(4x﹣x2)﹣m=﹣4x+m+2,
该函数与x轴只有一个交点,故舍去;
综上,m<6.


科目:初中数学 来源: 题型:
【题目】在一次数学活动课上,老师让同学们到操场上测量旗杆的高度,然后回来交流各自的测量方法.小芳的测量方法是:拿一根高3.5米的竹竿直立在离旗杆27米的C处(如图),然后沿BC方向走到D处,这时目测旗杆顶部A与竹竿顶部E恰好在同一直线上,又测得C、D两点的距离为3米,小芳的目高为1.5米,这样便可知道旗杆的高.你认为这种测量方法是否可行?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】工人师傅用一块长为10dm,宽为6dm的矩形铁皮制作一个无盖的长方体容器,需要将四角各裁掉一个正方形.(厚度不计)

(1)在图中画出裁剪示意图,用实线表示裁剪线,虚线表示折痕;并求长方体底面面积为12dm2时,裁掉的正方形边长多大?
(2)若要求制作的长方体的底面长不大于底面宽的五倍,并将容器进行防锈处理,侧面每平方分米的费用为0.5元,底面每平方分米的费用为2元,裁掉的正方形边长多大时,总费用最低,最低为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
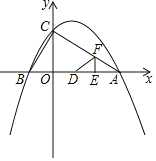
【题目】综合与探究:
已知二次函数y=﹣![]() x2+
x2+![]() x+2的图象与x轴交于A,B两点(点B在点A的左侧),与y轴交于点C.
x+2的图象与x轴交于A,B两点(点B在点A的左侧),与y轴交于点C.
(1)求点A,B,C的坐标;
(2)求证:△ABC为直角三角形;
(3)如图,动点E,F同时从点A出发,其中点E以每秒2个单位长度的速度沿AB边向终点B运动,点F以每秒![]() 个单位长度的速度沿射线AC方向运动.当点F停止运动时,点E随之停止运动.设运动时间为t秒,连结EF,将△AEF沿EF翻折,使点A落在点D处,得到△DEF.当点F在AC上时,是否存在某一时刻t,使得△DCO≌△BCO?(点D不与点B重合)若存在,求出t的值;若不存在,请说明理由.
个单位长度的速度沿射线AC方向运动.当点F停止运动时,点E随之停止运动.设运动时间为t秒,连结EF,将△AEF沿EF翻折,使点A落在点D处,得到△DEF.当点F在AC上时,是否存在某一时刻t,使得△DCO≌△BCO?(点D不与点B重合)若存在,求出t的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A是反比例图数y=![]() (x<0)图象上一点,AC⊥x轴于点C,与反比例函数y=
(x<0)图象上一点,AC⊥x轴于点C,与反比例函数y=![]() (x<0)图象交于点B,AB=2BC,连接OA、OB,若△OAB的面积为3,则m+n=( )
(x<0)图象交于点B,AB=2BC,连接OA、OB,若△OAB的面积为3,则m+n=( )
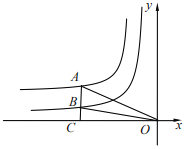
A.﹣4B.﹣6C.﹣8D.﹣12
查看答案和解析>>
科目:初中数学 来源: 题型:
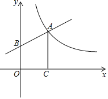
【题目】如图,已知点A在反比例函数![]() (x>0)的图像上,过点A作AC⊥x轴,垂足是C,AC=OC.一次函数y=kx+b的图像经过点A,与y轴的正半轴交于点B.
(x>0)的图像上,过点A作AC⊥x轴,垂足是C,AC=OC.一次函数y=kx+b的图像经过点A,与y轴的正半轴交于点B.
(1)求点A的坐标;
(2)若四边形ABOC的面积是![]() ,求一次函数y=kx+b的表达式.
,求一次函数y=kx+b的表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
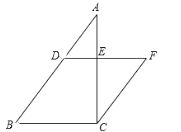
【题目】如图,在Rt△ABC中,∠ACB = 90°,BC = 6,AC = 8.点D是AB边上一点,过点D作DE // BC,交边AC于E.过点C作CF // AB,交DE的延长线于点F.
(1)如果![]() ,求线段EF的长;
,求线段EF的长;
(2)求∠CFE的正弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com