
 如图,在矩形ABCD中,AD=4,点P是直线AD上一动点,若满足△PBC是等腰三角形的点P有且只有3个,则AB的长为4或2$\sqrt{3}$.
如图,在矩形ABCD中,AD=4,点P是直线AD上一动点,若满足△PBC是等腰三角形的点P有且只有3个,则AB的长为4或2$\sqrt{3}$. 分析 要求直线AD上满足△PBC是等腰三角形的点P有且只有3个时的AB长,则需要分类讨论:①当AB=AD时;②当AB<AD时,③当AB>AD时.
解答 解:①如图,当AB=AD时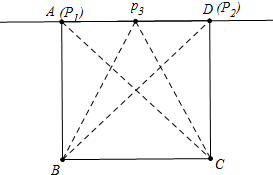
满足△PBC是等腰三角形的点P有且只有3个,
△P1BC,△P2BC是等腰直角三角形,△P3BC是等腰直角三角形(P3B=P3C),
则AB=AD=4.
②当AB<AD,且满足△PBC是等腰三角形的点P有且只有3个时,如图,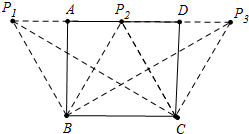
易知P2是AD的中点,BC=BP1=BP2=CP2=CP3
∴BP2=$\sqrt{{2}^{2}+A{B}^{2}}$=$\sqrt{4+A{B}^{2}}$,
又∵BP1=BC,
∴$\sqrt{4+A{B}^{2}}$=4
∴AB=2$\sqrt{3}$.
③当AB>AD时,直线AD上只有一个点P满足△PBC是等腰三角形.
故答案为:4或2$\sqrt{3}$.
点评 本题考查矩形的性质,等腰三角形的性质等知识,解题的关键是理解题意,属于中考常考题型.


科目:初中数学 来源: 题型:解答题
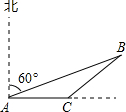 三国魏人刘徽,自撰《海岛算经》,专论测高望远.某校王老师根据《海岛算经》中的问题,编了这样一道题:如图,甲、乙两船同时由港口A出发开往海岛B,甲船沿北偏东60°方向向海岛B航行,其速度为15海里/小时;乙船速度为20海里/小时,先沿正东方向航行1小时后,到达C港口接旅客,在C港口停留0.5小时后再沿东北方向开往B岛,其速度仍为20海里/小时.B岛建有一座灯塔,在灯塔方圆5海里内都可以看见灯塔,问甲、乙两船哪一艘先看到灯塔,两船看到灯塔的时间相差多少?(精确到分钟,$\sqrt{3}$≈1.73,$\sqrt{2}$≈1.41)
三国魏人刘徽,自撰《海岛算经》,专论测高望远.某校王老师根据《海岛算经》中的问题,编了这样一道题:如图,甲、乙两船同时由港口A出发开往海岛B,甲船沿北偏东60°方向向海岛B航行,其速度为15海里/小时;乙船速度为20海里/小时,先沿正东方向航行1小时后,到达C港口接旅客,在C港口停留0.5小时后再沿东北方向开往B岛,其速度仍为20海里/小时.B岛建有一座灯塔,在灯塔方圆5海里内都可以看见灯塔,问甲、乙两船哪一艘先看到灯塔,两船看到灯塔的时间相差多少?(精确到分钟,$\sqrt{3}$≈1.73,$\sqrt{2}$≈1.41)查看答案和解析>>
科目:初中数学 来源: 题型:填空题
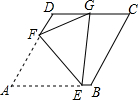 如图,已知菱形ABCD的边长2,∠A=60°,点E、F分别在边AB、AD上,若将△AEF沿直线EF折叠,使得点A恰好落在CD边的中点G处,则EF=$\frac{7\sqrt{21}}{20}$.
如图,已知菱形ABCD的边长2,∠A=60°,点E、F分别在边AB、AD上,若将△AEF沿直线EF折叠,使得点A恰好落在CD边的中点G处,则EF=$\frac{7\sqrt{21}}{20}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com