
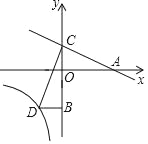
【题目】如图,直线y=kx+b过点A(5,0)和点C,反比例函数y=![]() (x<0)过点D,作BD∥x轴交y轴于点B(0,﹣3),且BD=OC,tan∠OAC=
(x<0)过点D,作BD∥x轴交y轴于点B(0,﹣3),且BD=OC,tan∠OAC=![]() .
.
(1)求反比例函数y=![]() (x<0)和直线y=kx+b的解析式;
(x<0)和直线y=kx+b的解析式;
(2)连接CD,判断线段AC与线段CD的关系,并说明理由.
【答案】(1)y=![]() ,y=﹣
,y=﹣![]() x+2;(2)AC⊥CD.
x+2;(2)AC⊥CD.
【解析】分析:(1)由A点坐标可求得OA的长,再利用三角函数的定义可求得OC的长,可求得C、D点坐标,再利用待定系数法可求得直线AC的解析式;
(2)由条件可证明△OAC≌△BCD,再由角的和差可求得∠OAC+∠BCA=90°,可证得AC⊥CD.
详解:(1)∵A(5,0),∴OA=5.
∵tan∠OAC=![]() =
=![]() .
.
解得:OC=2,∴C(0,2),∴BD=OC=2.
∵B(0,﹣3),BD∥x轴,∴D(﹣2,﹣3),∴m=﹣2×(﹣3)=6,∴y=![]() .
.
设直线AC关系式为y=kx+b.
∵过A(5,0),C(0,2),∴![]() ,
,
解得: ,∴y=﹣
,∴y=﹣![]() +2;
+2;
(2)∵B(0,﹣3),C(0,2),∴BC=5=OA.
∵x轴⊥y轴,∠AOC=∠COE=90°,BD∥x轴,
∴∠COE=∠DBC=90°,∴∠AOC=∠DBC.
在△OAC和△BCD中,
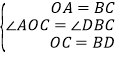
∴△OAC≌△BCD(SAS),
∴AC=CD,∴∠OAC=∠BCD,
∴∠BCD+∠BCA=∠OAC+∠BCA=90°,
∴AC⊥CD.



 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案科目:初中数学 来源: 题型:
【题目】州教育局为了解我州八年级学生参加社会实践活动情况,随机抽查了某县部分八年级学生第一学期参加社会实践活动的天数,并用得到的数据检测了两幅统计图,下面给出了两幅不完整的统计图(如图)

请根据图中提供的信息,回答下列问题:
(1)a= ,并写出该扇形所对圆心角的度数为 ,请补全条形图.
(2)在这次抽样调查中,众数和中位数分别是多少?
(3)如果该县共有八年级学生2000人,请你估计“活动时间不少于7天”的学生人数大约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一列数![]() ,a2,a3,…,
,a2,a3,…,![]() ,其中a1=-1,
,其中a1=-1,![]() ,
,![]() ,…,
,…,![]() ,完成下列填空:
,完成下列填空:
(1)a2 = ,a3 = ,a2019 = ;
(2)a1+a2+a3+……+a2019 = .(直接写出计算结果)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为4,点E、F分别在AB、BC上,且AE=BF=1,CE、DF交于点O,下列结论:①∠DOC=90°,②OC=OE,③CE=DF,④tan∠OCD=![]() ,⑤S△DOC=S四边形EOFB中,正确的有( )
,⑤S△DOC=S四边形EOFB中,正确的有( )
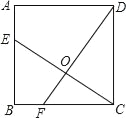
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某船从A码头顺流航行到B码头,然后逆流返行到C码头,共行9小时,已知船在静水中的速度为7.5千米/时,水流的速度为2.5千米/时,若A与C的距离为15千米,求A与B的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数y=2x+4
(1)在如图所示的平面直角坐标系中,画出函数的图象;

2)求图象与x轴的交点A的坐标,与y轴交点B的坐标;
(3)在(2)的条件下,求出△AOB的面积;
(4)利用图象直接写出:当y<0时,x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】结合数轴与绝对值的知识回答下列问题:
(1)数轴上表示4和1的两点之间的距离是 ;表示﹣3和2两点之间的距离是 ;一般地,数轴上表示数m和数n的两点之间的距离等于|m﹣n|.如果表示数a和﹣2的两点之间的距离是3,那么a= ;
(2)若数轴上表示数a的点位于﹣4与2之间,求|a+4|+|a﹣2|的值;
(3)当a取何值时,|a+5|+|a﹣1|+|a﹣4|的值最小,最小值是多少?请说明理由.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
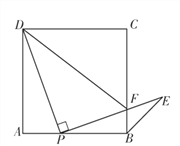
【题目】如图,点P是正方形ABCD边AB上一点(点P不与点A,B重合),连接PD,将线段PD绕点P顺时针方向旋转90°得到线段PE,PE交边BC于点F,连接BE,DF.
(1)求∠PBE的度数;
(2)若△PFD∽△BFP,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
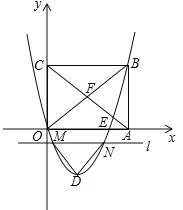
【题目】如图,在平面直角坐标系中,矩形OABC的边OA、OC分别在x轴、y轴上,点B坐标为(4,t)(t>0),二次函数![]() (b<0)的图象经过点B,顶点为点D.
(b<0)的图象经过点B,顶点为点D.
(1)当t=12时,顶点D到x轴的距离等于 ;
(2)点E是二次函数![]() (b<0)的图象与x轴的一个公共点(点E与点O不重合),求OEEA的最大值及取得最大值时的二次函数表达式;
(b<0)的图象与x轴的一个公共点(点E与点O不重合),求OEEA的最大值及取得最大值时的二次函数表达式;
(3)矩形OABC的对角线OB、AC交于点F,直线l平行于x轴,交二次函数![]() (b<0)的图象于点M、N,连接DM、DN,当△DMN≌△FOC时,求t的值.
(b<0)的图象于点M、N,连接DM、DN,当△DMN≌△FOC时,求t的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com