
����Ŀ����֪����ͼ1��ֱ��l1��x�ᣬֱ��l2Ϊ��һ�������Ľ�ƽ���ߣ�ֱ��l1��l2�ཻ��A��3��3������BΪֱԽl1��һ�㣬��CΪx����һ�㣬P��x��y��Ϊһ���㣮
��1������P��x��y����x����ʱ��y=��������������P��x��y����ֱ��l1�ϣ�y=��������������P��x��y����ֱ��l2��ʱy=����������
��ͼ1������P��ֱ��l1�·���x���Ϸ���ֱ��l2���Ϸ�����ʱ��x��y��������������![]() ������APO����PAB����POC��������ϵ������������
������APO����PAB����POC��������ϵ������������
��ͼ2������P��ֱ��l1�·���x���Ϸ���ֱ��l2���·�����ʱ��x��y��������������![]() ������APO����PAB����POC��������ϵ������������
������APO����PAB����POC��������ϵ������������
��2������P��ֱ��l1�Ϸ������ҵ�P����ֱ��l2ʱ��x��y���������Ϊ��![]() ���뻭��ͼ�Σ�������APO����PAB����POC��������ϵ����˵�����ɣ�
���뻭��ͼ�Σ�������APO����PAB����POC��������ϵ����˵�����ɣ�

���𰸡���1��0��3��x����APO����PAB����POC=360������APO=��PAB����POC��
��2����ͼ���������ٵ�P��ֱ��l1�Ϸ���ֱ��l2���Ϸ�����ʱ����PAB=��APO����POC���ڵ�P��ֱ��l1�Ϸ���ֱ��l2���·�����ʱ����POC=��APO����PAB�����ɼ�������
��������
��1�������l1�� l2�Ľ���ʽ������P�������ص㼴����⣻ͼ1�й�P����PQ��x�ᣬ����ƽ���ߵ����ʼ��ɵõ���APO����PAB����POC��������ϵ������ͼ��ͬ���ɵ���APO����PAB����POC��������ϵ��
��2����������ֱ���ͼ������ƽ���ߵ���������Ƕ���������⣮
��1����ֱ��l2Ϊ��һ�������Ľ�ƽ���ߣ�
��l2�Ľ���ʽΪy=x
��ֱ��l1��l2�ཻ��A��3��3����
��l1�Ľ���ʽΪy=3
�൱��P��x��y����x����ʱ��y=0������P��x��y����ֱ��l1�ϣ�y=3������P��x��y����ֱ��l2��ʱy=x��
��ͼ1����P����PQ��x�ᣬ
��PQ��x���l1��
���APQ����PAB=180������QPO����POC=180����
�֡�APQ����QPO=��APO
���APO����PAB����POC=360����
��ͼ2����P����PQ��x�ᣬ
��PQ��x���l1��
���APQ=��PAB����QPO=��POC��
�֡�APQ����QPO=��APO
���APO=��PAB����POC��
�ʴ�Ϊ��0��3��x����APO����PAB����POC=360������APO=��PAB����POC��

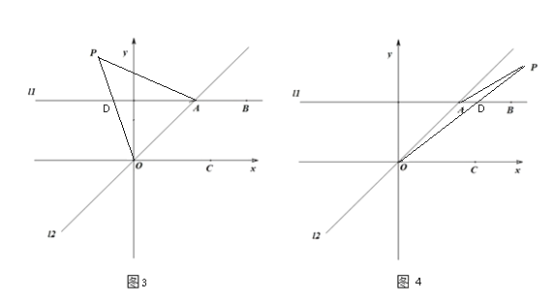
��2����ͼ3����P��ֱ��l1�Ϸ���ֱ��l2���Ϸ�����ʱ��
��x���l1
���POC=��PDB��
�֡�PAB=��APO����PDB��
���PAB=��APO����POC��
��ͼ4����P��ֱ��l1�Ϸ���ֱ��l2���·�����ʱ��
��x���l1
���POC=��PDB��
�֡�PDB =��APO����PAB��
���POC=��APO����PAB��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ͼ��ÿ��̨���϶�����һ���������µ��ϵĵ�1������4��̨�������α��ţ�5����2��1��9�������������ĸ�̨�������ĺͶ���ȣ�
��1�����5��̨���ϵ���![]() �Ƕ��٣�
�Ƕ��٣�
��2������µ���ǰ31��̨�������ĺͣ�
��3�����ú�![]() ��
��![]() Ϊ����������ʽ�ӱ�ʾ������1�����ڵ�̨������
Ϊ����������ʽ�ӱ�ʾ������1�����ڵ�̨������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ʽx![]() +2xy��y
+2xy��y![]() ����x
����x![]() ��y
��y![]() +2xy��x
+2xy��x![]() +xy+y
+xy+y![]() ��4x
��4x![]() +1+4x.����������ȫƽ����ʽ��ʽ�ֽ���У� ��
+1+4x.����������ȫƽ����ʽ��ʽ�ֽ���У� ��
A.1��B.2��C.3��D.4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ABC��ֱ������ϵ�ڣ��������������ֱ�ΪA��0��3����B��3��4����C��2��2����������������ÿ��С�����εı߳���Ϊһ����λ���ȣ���

�ٻ�����ABC����ƽ��4����λ���ȵõ�����A1B1C1 �� ��C1��������________��
���Ե�BΪλ�����ģ��������ڻ�����A2B2C2 �� ʹ��A2B2C2����ABCλ�ƣ���λ�Ʊ�Ϊ2��1����C2��������________��
����M��a��b��Ϊ�߶�AC����һ�㣬д����M�Ķ�Ӧ��M2������________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC �У�AB=AC����C=70�㣬��AB��C������ABC ����ֱ�� EF�Գƣ���CAF=10�㣬���� BB�������ABB���Ķ����ǣ� ��

A. 30�� B. 35�� C. 40�� D. 45��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ��y=kx+b��k��0����������y=ax2��a��0������A��B���㣬�ҵ�A�ĺ�������-2����B�ĺ�������3�������½��ۣ�
��������y=ax2��a��0����ͼ��Ķ���һ����ԭ�㣻
��x��0ʱ��ֱ��y=kx+b��k��0����������y=ax2��a��0���ĺ���ֵ������x�����������
��AB�ij��ȿ��Ե���5��
�ܡ�OAB�п��ܳ�Ϊ�ȱ������Σ�
����-3��x��2ʱ��ax2+kx��b��
������ȷ�Ľ����ǣ� ��

A. �٢ڢ� B. �٢ڢ� C. �ڢۢ� D. �ۢܢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����κ���y=��![]() x2+bx+c��ͼ��A��2��0����B��0����6��������
x2+bx+c��ͼ��A��2��0����B��0����6��������
��1����������κ����Ľ���ʽ��
��2����ö��κ����ĶԳ�����x�ύ�ڵ�C������BA��BC�����ABC�������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ͼ��٢ڢ۾�����P0ΪԲ�ģ�1����λ����Ϊ�뾶�����Σ���ͼ�٢ڢ۷ֱ��ض��������ϣ���������ͬʱƽ�ƣ�ÿ���ƶ�һ����λ���ȣ���һ���ƶ���ͼ�٢ڢ۵�Բ������ΪP1P2P3���ڶ����ƶ���ͼ�٢ڢ۵�Բ������ΪP4P5P6�������˹��ɣ�P0P2018=_____����λ���ȣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��pΪʵ��.
p | k | q |
�� | �� | �� |
3 | 16��3��26 | 2��2��6 |
4 | 16��4��26 | 2��3��7 |
5 | 16��5��26 | 2��4��8 |
6 | 16��6��26 | 2��5��9 |
7 | 16��7��26 | 2��6��10 |
�� | �� | �� |
�����ϱ��еĹ��ɣ��ش��������⣺
(1)��pΪ��ֵʱ��k��38?
(2)��pΪ��ֵʱ��k��q��ֵ��ȣ�
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com