
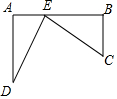
 如图,铁路上A,B两站(视为线上两点)相距25千米,C,D为铁路同旁两个村庄(视为两点),DA⊥AB于A点,CB⊥AB于B点,DA=15千米,CB=10千米,现在要在铁路AB上修一个土特品回购站E,使C,D两村庄到E站的距离相等,则E站应建在距A站10千米处.
如图,铁路上A,B两站(视为线上两点)相距25千米,C,D为铁路同旁两个村庄(视为两点),DA⊥AB于A点,CB⊥AB于B点,DA=15千米,CB=10千米,现在要在铁路AB上修一个土特品回购站E,使C,D两村庄到E站的距离相等,则E站应建在距A站10千米处.  黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案科目:初中数学 来源: 题型:解答题
 如图,AB是⊙O的一条弦,C,D是⊙O上的两个动点,且在AB弦的异侧,连接CD.
如图,AB是⊙O的一条弦,C,D是⊙O上的两个动点,且在AB弦的异侧,连接CD.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 今年5月8日母亲节那天,某班很多同学给妈妈准备了鲜花和礼盒,根据图中的信息
今年5月8日母亲节那天,某班很多同学给妈妈准备了鲜花和礼盒,根据图中的信息查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
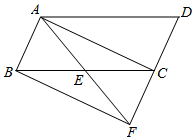 如图,已知E是平行四边形ABCD中BC边的中点,连接AE并延长AE交DC的延长线于点F.
如图,已知E是平行四边形ABCD中BC边的中点,连接AE并延长AE交DC的延长线于点F.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 调查市场上饮用水的质量情况 | |
| B. | 调查某品牌圆珠笔芯的使用寿命 | |
| C. | 调查乘坐飞机的旅客是否携带了危禁物品 | |
| D. | 调查我市市民每天的上网时长 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com