
【题目】已知⊙O的半径为12cm,弦AB=12![]() cm.
cm.
(1)求圆心O到弦AB的距离.
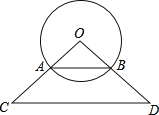
(2)若弦AB恰好是△OCD的中位线,以CD中点E为圆点,R为半径作⊙E,当⊙O和⊙E相切时,求R的值.
【答案】(1) ![]() cm;(2) 分为两种情况:当两圆外切时,半径
cm;(2) 分为两种情况:当两圆外切时,半径![]() cm,当两圆内切时,半径
cm,当两圆内切时,半径![]() cm.
cm.
【解析】分析:(1)过O作OF⊥AB于F,交CD于E,根据等腰三角形性质求出AF,根据勾股定理求出OF即可;
(2)求出OE,求出EM和EN,即可得出答案.
本题解析::(1)过O作OF⊥AB于F,交CD于E,
∵OA=OB,
∴AF=BF=![]() AB=
AB=![]() ×12
×12![]() cm=6
cm=6![]() cm,
cm,
在Rt△OAF中,由勾股定理得:OF=![]() (cm),
(cm),
即圆心O到弦AB的距离是6![]() cm;
cm;
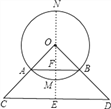
(2)∵OF=AF=6![]() cm,
cm,
∴∠OAB=45°,
∵AB是△OCD的中位线,
∴CD=2AB=24![]() cm,
cm,
∴OF=EF=6![]() cm,
cm,
即ME=OE-0M=6![]() +6
+6![]() -12=(12
-12=(12![]() -12)cm,
-12)cm,
分为两种情况:当两圆外切时,半径R=ME=(12![]() -12)cm,
-12)cm,
当两圆内切时,半径R=EN=(12![]() +12)cm.
+12)cm.


科目:初中数学 来源: 题型:
【题目】你会玩“24点”游戏吗?从一副扑克牌(去掉大、小王)中任意抽取4张,根据牌面上的数字,添加+、一、×、÷和括号等符号进行运算,每张牌只能用一次,使得运算结果为24,其中A、J、Q、K分别代表1,11,12,13.
(1)小明抽到的是如下4张牌,你凑成24的算式是______(写出一个即可).

(2)现有四个有理数3、4、 -6、10,运用上述规则写出两种不同方法的运算式,使其结果等于24.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把下列各数填入它所属的集合内:5.2,0,![]() ,
,![]() ,+(﹣4),﹣2
,+(﹣4),﹣2![]() ,﹣(﹣3 ),0.25555…,﹣0.030030003…
,﹣(﹣3 ),0.25555…,﹣0.030030003…
(1)分数集合:{_________________________________________ …}
(2)非负整数集合:{_________________________________________ …}
(3)有理数集合:{_________________________________________…}.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料:
解方程:x4﹣6x2+5=0.这是一个一元四次方程,根据该方程的特点,它的解法通常是:
设x2=y,那么x4=y2,于是原方程可变为y2﹣6y+5=0…①,
解这个方程得:y1=1,y2=5.
当y=1时,x2=1,∴x=±1;
当y=5时,x2=5,∴x=±![]()
所以原方程有四个根:x1=1,x2=﹣1,x3=![]() ,x4=﹣
,x4=﹣![]() .
.
在这个过程中,我们利用换元法达到降次的目的,体现了转化的数学思想.
(1)解方程(x2﹣x)2﹣4(x2﹣x)﹣12=0时,若设y=x2﹣x,则原方程可转化为 ;求出x
(2)利用换元法解方程:![]() =2.
=2.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】线段AB和线段CD交于点O,OE平分∠AOC,点F为线段AB上一点(不与点A和点O重合)过点F作 FG//OE,交线段CD于点G,若∠AOD=110°,则∠AFG的度数为_____°.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知∠MAN=30°,点B在射线AM上,且 AB=6,点C在射线AN上.

(1)若△ABC是直角三角形,求AC的长;
(2)若△ABC是等腰三角形,则满足条件的C点有 个;
(3)设BC=x,当△ABC唯一确定时, 直接写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国![]() 道路交通安全法
道路交通安全法![]() 第四十七条规定“机动车行经人行横道时,应当减速行驶;遇行人通过人行横道,应当停车让行”
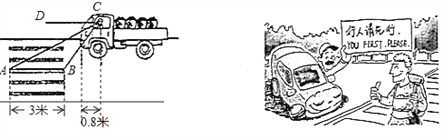
第四十七条规定“机动车行经人行横道时,应当减速行驶;遇行人通过人行横道,应当停车让行” ![]() 如图:一辆汽车在一个十字路口遇到行人时刹车停下,汽车里的驾驶员看地面的斑马线前后两端的视角分别是
如图:一辆汽车在一个十字路口遇到行人时刹车停下,汽车里的驾驶员看地面的斑马线前后两端的视角分别是![]() 和
和![]() ,如果斑马线的宽度是
,如果斑马线的宽度是![]() 米,驾驶员与车头的距离是
米,驾驶员与车头的距离是![]() 米,这时汽车车头与斑马线的距离x是多少?
米,这时汽车车头与斑马线的距离x是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场服装柜在销售中发现:某品牌童装平均每天可售出20件,每件盈利40元.为了迎接“六一”国际儿童节,商场决定采取适当的降价措施,扩大销售量,增加盈利,尽量减少库存.经市场调查发现:如果每件童装降价1元,那么平均每天就可多售出2件.假设商场降价![]() 元,
元,
(1)降价![]() 元后,每一件童装的利润为___________(元),每天可以卖出去的童装件数为____________(件)(用含
元后,每一件童装的利润为___________(元),每天可以卖出去的童装件数为____________(件)(用含![]() 的代数式表示);
的代数式表示);
(2)若销售该童装每天盈利要达到1200元,则每件童装应该降价多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
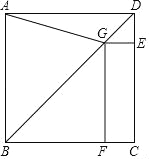
【题目】如图,在正方形ABCD中,点G在对角线BD上(不与点B,D重合),GE⊥DC于点E,GF⊥BC于点F,连结AG.
(1)写出线段AG,GE,GF长度之间的数量关系,并说明理由;
(2)若正方形ABCD的边长为1,∠AGF=105°,求线段BG的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com