
【题目】已知抛物线y=﹣x2+2nx﹣n2+n的顶点为P,直线y=![]() 分别交x,y轴于点M,N.
分别交x,y轴于点M,N.
(1)若点P在直线MN上,求n的值;
(2)是否存在过(0,﹣2)的直线与抛物线交于A,B两点(A点在B点的下方),使AB为定长,若存在,求出AB的长;若不存在,请说明理由;
(3)在(2)的条件下,当四边形MABN的周长最小时,求n的值.
【答案】(1) n=![]() ;(2) 存在直线y=x﹣2,使AB为定长,且AB=
;(2) 存在直线y=x﹣2,使AB为定长,且AB=![]() ;(3) n=1
;(3) n=1
【解析】
(1)利用配方法求出顶点P的坐标,利用待定系数法即可解决问题;
(2)设过(0,﹣2)的直线为y=kx﹣2,设A(x1,y1),B(x2,y2),利用k,n表示线段AB,构建方程求出k即可解决问题;
(3)由题意:M(﹣3,0),N(0,![]() ),如图,平移AB,使A点于M点重合,则B的对应点G刚好落在y轴上,且G(0,3).作点G关于直线y=x﹣2的对称点H(5,﹣2).连接NH交直线y=x﹣2为点R(2,0).可证明当点B与R重合时,四边形MABN的周长最小.利用待定系数法即可解决问题.
),如图,平移AB,使A点于M点重合,则B的对应点G刚好落在y轴上,且G(0,3).作点G关于直线y=x﹣2的对称点H(5,﹣2).连接NH交直线y=x﹣2为点R(2,0).可证明当点B与R重合时,四边形MABN的周长最小.利用待定系数法即可解决问题.
(1)∵y=﹣x2+2nx﹣n2+n=﹣(x﹣n)2+n,∴顶点P(n,n),把P(n,n)代入![]() ,得n=
,得n=![]() .
.
(2)设过(0,﹣2)的直线为y=kx﹣2,设A(x1,y1),B(x2,y2).
联立![]() ,消元得x2+(k﹣2n)x+n2﹣n﹣2=0,∴
,消元得x2+(k﹣2n)x+n2﹣n﹣2=0,∴![]() ,∴
,∴![]() ,∴y1﹣y2=k(x1﹣x2),∴(y1﹣y2)2=k2(x1﹣x2)2,∴AB2=(x1﹣x2)2+(y1﹣y2)2=(1+k2)[k2+8+(4﹣4k)n].
,∴y1﹣y2=k(x1﹣x2),∴(y1﹣y2)2=k2(x1﹣x2)2,∴AB2=(x1﹣x2)2+(y1﹣y2)2=(1+k2)[k2+8+(4﹣4k)n].
∵要使AB为定长,则AB2的值与n的取值无关,∴4﹣4k=0,∴k=1,∴存在直线y=x﹣2,使AB为定长,且AB=![]() .
.
(3)由题意:M(﹣3,0),N(0,![]() ),如图,平移AB,使A点于M点重合,则B的对应点G刚好落在y轴上,且G(0,3).作点G关于直线y=x﹣2的对称点H(5,﹣2).
),如图,平移AB,使A点于M点重合,则B的对应点G刚好落在y轴上,且G(0,3).作点G关于直线y=x﹣2的对称点H(5,﹣2).
连接NH交直线y=x﹣2为点R(2,0).
可证明当点B与R重合时,四边形MABN的周长最小.
将 R(2,0)代入y=﹣(x﹣n)2+n中,得:n1=1,n2=4(舍去),∴n=1.


科目:初中数学 来源: 题型:
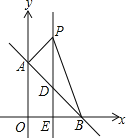
【题目】如图,平面直角坐标系中,直线AB:y=﹣x+b交y轴于点A(0,4),交x轴于点B.
(1)求直线AB的表达式和点B的坐标;
(2)直线l垂直平分OB交AB于点D,交x轴于点E,点P是直线l上一动点,且在点D的上方,设点P的纵坐标为n.
①用含n的代数式表示△ABP的面积;
②当S△ABP=8时,求点P的坐标;
③在②的条件下,以PB为斜边在第一象限作等腰直角△PBC,求点C的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】工人师傅用一块长为10dm,宽为6dm的矩形铁皮制作一个无盖的长方体容器,需要将四角各裁掉一个正方形.(厚度不计)

(1)在图中画出裁剪示意图,用实线表示裁剪线,虚线表示折痕;并求长方体底面面积为12dm2时,裁掉的正方形边长多大?
(2)若要求制作的长方体的底面长不大于底面宽的五倍,并将容器进行防锈处理,侧面每平方分米的费用为0.5元,底面每平方分米的费用为2元,裁掉的正方形边长多大时,总费用最低,最低为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:在平面直角坐标系中,点![]() 为坐标原点,
为坐标原点,![]() 的顶点
的顶点![]() 的坐标为
的坐标为![]() ,顶点
,顶点![]() 在
在![]() 轴上(点
轴上(点![]() 在点
在点![]() 的右侧),点
的右侧),点![]() 在
在![]() 上,连接
上,连接![]() ,且
,且![]() .
.
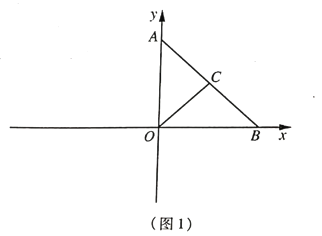
(1)如图1,求点![]() 的纵坐标;
的纵坐标;
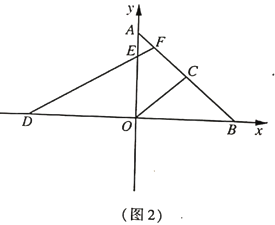
(2)如图2,点![]() 在
在![]() 轴上(点
轴上(点![]() 在点
在点![]() 的左侧),点
的左侧),点![]() 在
在![]() 上,连接
上,连接![]() 交
交![]() 于点
于点![]() ;若
;若![]() ,求证:
,求证:![]()
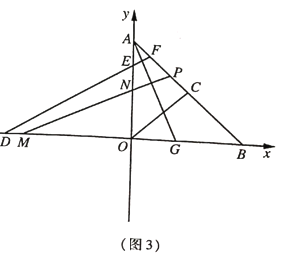
(3)如图3,在(2)的条件下,![]() 是
是![]() 的角平分线,点
的角平分线,点![]() 与点
与点![]() 关于
关于![]() 轴对称,过点
轴对称,过点![]() 作
作![]() 分别交
分别交![]() 于点
于点![]() ,若
,若![]() ,求点
,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC,∠ACB=90°,AC=BC=4,D是AB的中点,P是平面上的一点,且DP=1,连接BP,CP
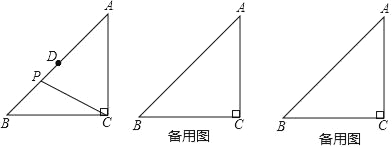
(1)如图,当点P在线段BD上时,求CP的长;
(2)当△BPC是等腰三角形时,求CP的长;
(3)将点B绕点P顺时针旋转90°得到点B′,连接AB′,求AB′的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=8,BC=6,P为AD上一点,将△ABP沿BP翻折至△EBP,PE与CD相交于点O,BE与CD相交于点G,且OE=OD,则AP的长为______.
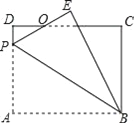
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,AB为⊙O的直径,点C、D在⊙O上,且BC=6cm,AC=8cm,∠ABD=45°.

(1)求BD的长;
(2)求图中阴影部分的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com