
分析 (1)(2)(3)(4)直接利用多项式乘多项式的法则计算即可;
(5)先利用多项式乘多项式的法则计算,再去括号、合并同类项即可.
解答 解:(1)(x+5)(x+1)=x2+x+5x+5=x2+6x+5;
(2)(3a+b)(a-2b)=3a2-6ab+ab-2b2=3a2-5ab-2b2;
(3)($\frac{1}{2}$x+2)(4x-$\frac{1}{2}$)=2x2-$\frac{1}{4}$x+8x-1=2x2+$\frac{31}{4}$x-1;
(4)(x2+xy+y2)(x-y)=x3+x2y+xy2-x2y-xy2-y3=x3-y3;
(5)(x-1)(x+3)-2(x-5)(x-2)
=(x2+3x-x-3)-2(x2-7x+10)
=x2+2x-3-2x2+14x-20
=-x2+16x-23.
点评 本题主要考查了多项式与多项式相乘的法则:多项式与多项式相乘,先用一个多项式的每一项乘另外一个多项式的每一项,再把所得的积相加.运用法则时应注意以下两点:①相乘时,按一定的顺序进行,必须做到不重不漏;②多项式与多项式相乘,仍得多项式,在合并同类项之前,积的项数应等于原多项式的项数之积.


 金博士一点全通系列答案
金博士一点全通系列答案科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | 0 | C. | -$\frac{1}{2}$ | D. | -$\frac{1}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
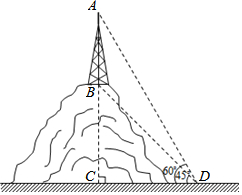 如图,某山顶上建有手机信号中转塔AB,在地面D处测得塔尖的仰角∠ADC=60°,塔底的仰角∠BDC=45°,点D距离塔AB所在直线的距离DC为100米,求手机信号中转塔AB的高度(参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732,结果保留整数).
如图,某山顶上建有手机信号中转塔AB,在地面D处测得塔尖的仰角∠ADC=60°,塔底的仰角∠BDC=45°,点D距离塔AB所在直线的距离DC为100米,求手机信号中转塔AB的高度(参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732,结果保留整数).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
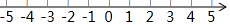
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,点A、B和线段MN都在数轴上,点A、M、N、B对应的数字分别为-1、0、2、11.线段MN沿数轴的正方向以每秒1个单位的速度移动,移动时间为t秒.
如图,点A、B和线段MN都在数轴上,点A、M、N、B对应的数字分别为-1、0、2、11.线段MN沿数轴的正方向以每秒1个单位的速度移动,移动时间为t秒.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在△ABC中,DE∥BC,AD=4,DE=3,DB=8.
如图,在△ABC中,DE∥BC,AD=4,DE=3,DB=8.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com