
 ,垂足为E.
,垂足为E.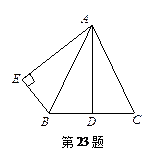
|
 ,
,


科目:初中数学 来源: 题型:
(本题满分13分)如图,在梯形ABCD中,AD∥BC,∠B=90°,BC=6,AD=3,∠DCB=30°.点E、F同时从B点出发,沿射线BC向右匀速移动.已知F点移动速度是E点移动速度的2倍,以EF为一边在CB的上方作等边△EFG.设E点移动距离为x(x>0).

⑴△EFG的边长是____(用含有x的代数式表示),当x=2时,点G的位置在_______;
⑵若△EFG与梯形ABCD重叠部分面积是y,求
①当0<x≤2时,y与x之间的函数关系式;
②当2<x≤6时,y与x之间的函数关系式;
⑶探求⑵中得到的函数y在x取含何值时,存在最大值,并求出最大值.
查看答案和解析>>
科目:初中数学 来源:2010年湖北省黄冈市初一上学期期末模拟数学卷 题型:解答题
(本题满分13分)
已知:如图,AB=AC,点D是BC的中点,AB平分∠DAE, ,垂足为E.
,垂足为E.
(1)求证:AD=AE.
(2)若BE∥AC,试判断△ABC的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源:2010年高级中等学校招生考试数学卷(广东珠海) 题型:解答题
(本题满分13分)如图,在梯形ABCD中,AD∥BC,∠B=90°,BC=6,AD=3,∠DCB=30°.点E、F同时从B点出发,沿射线BC向右匀速移动.已知F点移动速度是E点移动速度的2倍,以EF为一边在CB的上方作等边△EFG.设E点移动距离为x(x>0).

⑴△EFG的边长是____(用含有x的代数式表示),当x=2时,点G的位置在_______;
⑵若△EFG与梯形ABCD重叠部分面积是y,求
①当0<x≤2时,y与x之间的函数关系式;
②当2<x≤6时,y与x之间的函数关系式;
⑶探求⑵中得到的函数y在x取含何值时,存在最大值,并求出最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com