
【题目】如图,在平面直角坐标系第一象限中,已知点A坐标为(1,0),点D坐标为(1,3),点G坐标为(1,1),动点E从点G出发,以每秒1个单位长度的速度匀速向点D方向运动,与此同时,x轴上动点B从点A出发,以相同的速度向右运动,两动点运动时间为t(0<t<2),以AD、AB分别为边作矩形ABCD,过点E作双曲线交线段BC于点F,作CD中点M,连接BE、EF、EM、FM.
(1)当t=1时,求点F的坐标.
(2)若BE平分∠AEF,则t的值为多少?
(3)若∠EMF为直角,则t的值为多少?

【答案】(1)点F(2,1);(2)t=![]() ;(3)t=4
;(3)t=4![]() ﹣4
﹣4
【解析】
(1)t=1时,可以求出E点坐标(1,2),并算出经过它的双曲线解析式![]() ,F点和B点的横坐标相同,把B点横坐标x=2代入就可算出F点坐标.
,F点和B点的横坐标相同,把B点横坐标x=2代入就可算出F点坐标.
(2)因为AE![]() BC,所以
BC,所以![]() ,又因为EB平分
,又因为EB平分![]() ,所以
,所以![]() , EF=BF, 在通过坐标用含t的代数式表示EF和BF的长,建立等量关系就可以算出t的值.
, EF=BF, 在通过坐标用含t的代数式表示EF和BF的长,建立等量关系就可以算出t的值.
(3)通过坐标用含t的代数式分别表示出EM,MF,EF的长,因为![]() 是直角,所以
是直角,所以![]() 是直角三角形,运用勾股定理
是直角三角形,运用勾股定理![]() 建立等量关系,算出t即可.
建立等量关系,算出t即可.
(1)t=1时,E点坐标为(1,2),F点横坐标x=2,
设经过E的双曲线为![]() ,
,
把E点坐标代入得:![]() ,
,
再把F点横坐标x=2代入![]() ,
,
得y=1,所以F点坐标为(2,1).
(2)因为A点坐标为(1,0),G点坐标为(1,1),
则t秒后,E点坐标可以表示为(1,1+t),
B点坐标可以表示为(1+t,0),
设经过E点双曲线为:![]() ,
,
把E点坐标代入得:![]() ,
,
F点也在双曲线上,F点横坐标和B相同,
把x=1+t代入函数![]() 得,
得,
y=1,所以F点坐标为(1+t,1),
因为AE![]() BC,所以
BC,所以![]() ,
,
又EB平分![]() ,所以
,所以![]() , EF=BF,
, EF=BF,
即![]() ,
,
解得t=![]() .
.
(3)因为D点坐标为(1,3),M为DC中点,则M点坐标为(1,![]() ),
),
又![]() 是直角,所以
是直角,所以![]() 是直角三角形,
是直角三角形,
由勾股定理![]() ,
,
得:![]() ,
,
解得t=![]() .
.


 智慧小复习系列答案
智慧小复习系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,点
中,点![]() 的坐标为(0,4),线段
的坐标为(0,4),线段![]() 的位置如图所示,其中点
的位置如图所示,其中点![]() 的坐标为(
的坐标为(![]() ,
,![]() ),点
),点![]() 的坐标为(3,
的坐标为(3,![]() ).
).

(1)将线段![]() 平移得到线段
平移得到线段![]() ,其中点
,其中点![]() 的对应点为
的对应点为![]() ,点
,点![]() 的对应点为点
的对应点为点![]() .
.
①点![]() 平移到点
平移到点![]() 的过程可以是:先向 平移 个单位长度,再向 平移 个单位长度;
的过程可以是:先向 平移 个单位长度,再向 平移 个单位长度;
②点![]() 的坐标为 .
的坐标为 .
(2)在(1)的条件下,若点![]() 的坐标为(4,0),连接
的坐标为(4,0),连接![]() ,画出图形并求
,画出图形并求![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,D、E分别是AC、AB上的点,BD与CE交于点O.给出下列三个条件:
①∠EBO=∠DCO;②∠BEO=∠CDO;③BE=CD.
(1)上述三个条件中,哪两个条件 可判定△ABC是等腰三角形(用序号写出所有情形);
(2)选择第(1)小题中的一种情形,证明△ABC是等腰三角形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在初中阶段的函数学习中,我们经历了“确定函数的表达式﹣﹣利用函数图象研究其性质一运用函数解决问题“的学习过程.在画函数图象时,我们通过描点或平移的方法画出了所学的函数图象.同时,我们也学习了绝对值的意义|a|=![]() .
.
结合上面经历的学习过程,现在来解决下面的问题:在函数y=|kx﹣1|+b中,当x=1时,y=3,当x=0时,y=4.
(1)求这个函数的表达式;
(2)在给出的平面直角坐标系中,请用你喜欢的方法画出这个函数的图象;
(3)已知函数y=![]() 的图象如图所示,结合你所画的函数图象,直接写出不等式|kx﹣1|+b≥
的图象如图所示,结合你所画的函数图象,直接写出不等式|kx﹣1|+b≥![]() 的解集.
的解集.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】苏州太湖养殖场计划养殖蟹和贝类产品,这两个品种的种苗的总投放量只有50吨,根据经验测算,这两个品种的种苗每投放一吨的先期投资,养殖期间的投资以及产值如下表(单位:万元/吨)
品种 | 先期投资 | 养殖期间投资 | 产值 |
贝类产品 | 0.9 | 0.3 | 0.33 |
蟹产品 | 0.4 | 1 | 2 |
养殖场受经济条件的影响,先期投资不超过36万元,养殖期间的投资不超过29万元,设贝类的种苗投放量为x吨,
(1)求x的取值范围;
(2)设这两个品种产出后的总产值为y(万元),试写出y与x之间的函数关系式,并求出当x等于多少时,y有最大值?最大值是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学为促进课堂教学,提高教学质量,对七年级学生进行了一次“你最喜欢的课堂教学方式”的问卷调查.根据收回的问卷,学校绘制了如下图表,请你根据图表中提供的信息,解答下列问题.
编号 | 教学方式 | 最喜欢的频数 | 频率 |
1 | 教师讲,学生听 | 20 | 0.10 |
2 | 教师提出问题,学生探索思考 | ||
3 | 学生自行阅读教材,独立思考 | 30 | |
4 | 分组讨论,解决问题 | 0.25 |
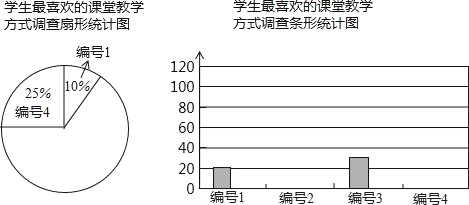
(1)收回的问卷份数为 ,把条形统计图补充完整;
(2)扇形统计图中编号1与编号4的圆心角分别是多少度?
(3)你最喜欢以上哪一种教学方式,请提出你的建议,并简要说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法中正确的是 ( )
A. 在 Rt△ABC中,若tanA=![]() ,则a=4,b=3
,则a=4,b=3
B. 在 Rt△ABC中,∠C=90°,则tanA+tanB=1
C. 在 Rt△ABC 中,∠C=90°,若a=3,b=4,则tanA=![]()
D. tan75°=tan(45°+30°)=tan45°+tan30°=1+![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司为奖励在趣味运动会上取得好成绩的员工,计划购买甲、乙两种奖品共20件,其中甲种奖品每件40元,乙种奖品每件30元.
(1)如果购买甲、乙两种奖品共花费了650元,求甲、乙两种奖品各购买了多少件;
(2)如果购买乙种奖品的件数不超过甲种奖品件数的2倍,总花费不超过680元,求该公司有哪几种不同的购买方案.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com