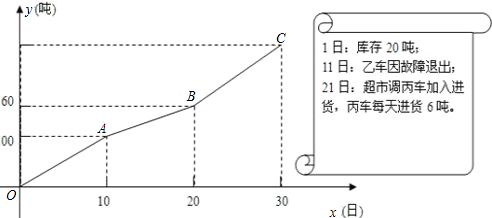
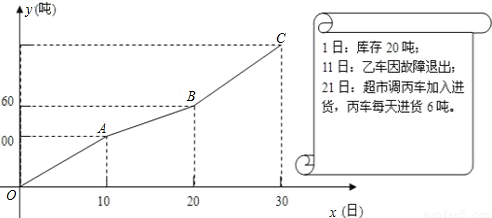
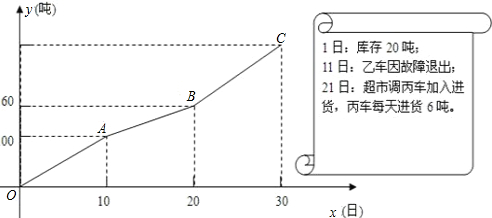
解:(1)根据图象,a=(160-100)÷(20-10)=6,
b=(100-0)÷(10-0)-a=4;
(2)∵甲、丙两车每天分别进货6吨、6吨,
∴甲、丙两车10天一共进货:(6+6)×10=120吨.
120+160=280.
设BC的解析式为y=Ax+B(20≤x≤30).
分别将B(20,160),C(30,280)代入解析式,
得二元一次方程组
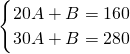
,
解得:
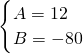
.
则线段BC的解析式为:y=12x-80(20≤x≤30);
(3)设商店x天共进货y吨,货源充足的情况下共出售货物z吨,库存P=y-z.
0≤x≤10时,P=10x+20-10x=20>0,此时供大于求;
11≤x≤20时,P=6(x-10)+10×10+20-10x=-4x+60
由P<0得15<x≤20,则11≤x≤20时,有5天时间供不应求;
20≤x≤26时,实际剩余存货P′=12(x-20)-10(x-20)=2x-40
第27天起初存货P′=2×26-40=12(吨);
27≤x≤30时,剩余存货P″=12(x-26)-15(x-26)+12=-3x+90
由P″=-3x+90<0得x>30,即27≤x≤30时,没有出现供不应求的情况;
综上所述,超市商品供不应求的天数为5天.
分析:(1)根据图10~20天这段时间内只有甲车负责进货便可求出a的值,再根据0~10天的时间段内求出a+b的值,进而得出b的值;
(2)设出AB段的解析式并分别代入A、B两点的坐标求出解析式,注明X的取值范围;
(3)分别求出日销量为10吨、15吨时,总销售量关于日销售量的函数求出两线段与图象中一次函数的交点,进而得出答案.
点评:本题考查一次函数的实际应用问题,解决此类问题应具备对一次函数图形的理解分析能力.

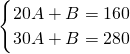 ,
,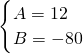 .
.

 新编小学单元自测题系列答案
新编小学单元自测题系列答案 字词句段篇系列答案
字词句段篇系列答案