
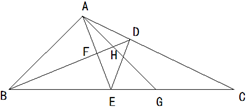
| A.1 | B.2 | C.3 | D.4 |


科目:初中数学 来源:不详 题型:单选题
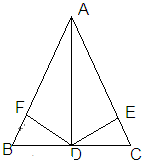
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
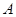 处6米处折断倒下,量得树梢
处6米处折断倒下,量得树梢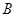 处与树底
处与树底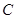 处的长是8米,树干
处的长是8米,树干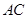 与地面
与地面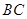 垂直.试通过计算求出这棵大树原来的高度.
垂直.试通过计算求出这棵大树原来的高度.
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
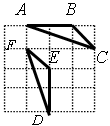
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
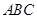 ,使其底角∠B=a,腰长AB =" c," 要求仅用直尺和圆规作图,并保留作图痕迹. (不写作法)
,使其底角∠B=a,腰长AB =" c," 要求仅用直尺和圆规作图,并保留作图痕迹. (不写作法)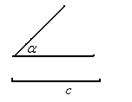
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com