
科目:初中数学 来源: 题型:解答题
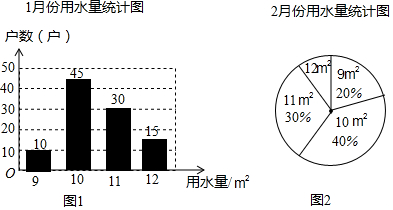
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
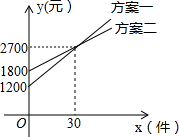 某公司推销一种产品,公司付给推销员的月报销有两种方案如图所示.设推销员推销产品的数量为x(件),付给推销员的月报酬为y(元).若公司决定改进“方案二”,保持基本工资不变,每件报酬增加m元,使得当销售员销售产品达到40件时,两种方案的报酬差额不超过100元,则m的取值范围是2.5≤m≤7.5.
某公司推销一种产品,公司付给推销员的月报销有两种方案如图所示.设推销员推销产品的数量为x(件),付给推销员的月报酬为y(元).若公司决定改进“方案二”,保持基本工资不变,每件报酬增加m元,使得当销售员销售产品达到40件时,两种方案的报酬差额不超过100元,则m的取值范围是2.5≤m≤7.5.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
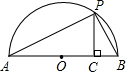 已知a、b是正实数,那么,$\frac{a+b}{2}$$≥\sqrt{ab}$是恒成立的.
已知a、b是正实数,那么,$\frac{a+b}{2}$$≥\sqrt{ab}$是恒成立的.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
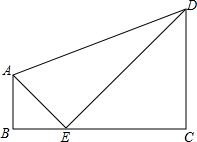 如图,已知直角梯形ABCD中,∠ABC=∠DCB=90°,点E在高上,且BE=AB=a,CE=CD=b,
如图,已知直角梯形ABCD中,∠ABC=∠DCB=90°,点E在高上,且BE=AB=a,CE=CD=b,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
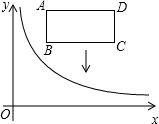 如图,在平面直角坐标系中,反比例函数y=$\frac{k}{x}$ (x>0)的图象和矩形ABCD在第一象限,AD平行于x轴,且AB=2,AD=4,点A的坐标为(2,6).
如图,在平面直角坐标系中,反比例函数y=$\frac{k}{x}$ (x>0)的图象和矩形ABCD在第一象限,AD平行于x轴,且AB=2,AD=4,点A的坐标为(2,6).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
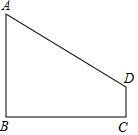 如图,AB⊥BC,DC⊥BC,垂足分别为B、C,设AB=4,DC=1,BC=4.
如图,AB⊥BC,DC⊥BC,垂足分别为B、C,设AB=4,DC=1,BC=4.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com