
【题目】如图,直线 AB,CD 相交于点O,OE 平分∠AOD,OF⊥OC.
(1)图中∠AOF 的余角是 (把符合条件的角都填出来);
(2)如果∠AOC=130°36′,那么根据 ,可得∠BOD= °;
(3)如果∠1与∠3的度数之比为3:4,求∠EOC和∠2的度数.
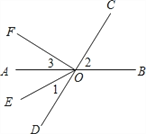
【答案】(1)∠AOD,∠COB;(2)对顶角相等,130.6°;(3)∠EOC=153°,∠2=54°
【解析】试题分析:(1)根据余角定义即可得出结论;
(2)根据对顶角相等得出结论;
(3)设一份为x,表示出∠1和∠3,由邻补角的定义得出∠EOC的度数,由角平分线定义及对顶角的性质得出∠2的度数.
试题解析:解:(1)∵OF⊥OC,∴∠AOF+∠COB=90°,∠AOF+∠AOD=90°,∴∠AOF的余角是∠AOD和∠COB;
(2)∵∠AOC=130°36′=130.6°,∴∠BOD=130.6°(对顶角相等);
(3)设∠1=3x,则∠3=4x,∵OE 平分∠AOD,∴∠AOE=∠DOE=3x,∵∠FOD=90°,∴3x+3x+4x=90°,∴x=9°,∴∠EOD=3x=27°,∴∠EOC=180°-∠EOD=180°-27°=153°.∵∠EOD=3x=27°,∠2=∠AOD=2∠EOD=2×27°=54°.


科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是平行四边形,E、F是对角线AC上的两点,∠1=∠2. 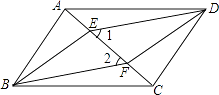
(1)求证:AE=CF;
(2)求证:四边形EBFD是平行四边形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,点E,F是对角线BD上两点,DE=BF. 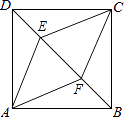
(1)判断四边形AECF是什么特殊四边形,并证明;
(2)若EF=4,DE=BF=2,求四边形AECF的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某频数分布直方图中,共有A、B、C、D、E五个小组,频数分布为10、15、25、35、10,则直方图中,长方形高的比为( )
A.2﹕3﹕5﹕7﹕2
B.1﹕3﹕4﹕5﹕1
C.2﹕3﹕5﹕6﹕2
D.2﹕4﹕5﹕4﹕2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com