
科目:初中数学 来源: 题型:解答题
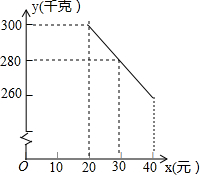 草莓是云南多地盛产的一种水果,今年某水果销售店在草莓销售旺季,试销售成本为每千克20元的草莓,规定试销期间销售单价不低于成本单价,也不高于每千克40元,经试销发现,销售量y(千克)与销售单价x(元)符合一次函数关系,如图是y与x的函数关系图象.
草莓是云南多地盛产的一种水果,今年某水果销售店在草莓销售旺季,试销售成本为每千克20元的草莓,规定试销期间销售单价不低于成本单价,也不高于每千克40元,经试销发现,销售量y(千克)与销售单价x(元)符合一次函数关系,如图是y与x的函数关系图象.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
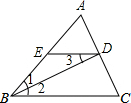 如图,△ABC中,BA=BC,BD是三角形的角平分线,DE∥BC交AB于E,下列结论:①∠1=∠3;②DE=$\frac{1}{2}$AB;③S△ADE=$\frac{1}{4}$S△ABC.正确的有( )
如图,△ABC中,BA=BC,BD是三角形的角平分线,DE∥BC交AB于E,下列结论:①∠1=∠3;②DE=$\frac{1}{2}$AB;③S△ADE=$\frac{1}{4}$S△ABC.正确的有( )| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
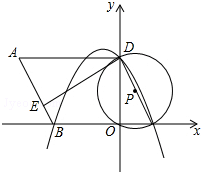 如图,在平面直角坐标系中,O为原点,平行四边形ABCD的边BC在x轴上,D点在y轴上,C点坐标为(2,0),BC=6,∠BCD=60°,点E是AB上一点,AE=3EB,⊙P过D,O,C三点,抛物线y=ax2+bx+c过点D,B,C三点.
如图,在平面直角坐标系中,O为原点,平行四边形ABCD的边BC在x轴上,D点在y轴上,C点坐标为(2,0),BC=6,∠BCD=60°,点E是AB上一点,AE=3EB,⊙P过D,O,C三点,抛物线y=ax2+bx+c过点D,B,C三点.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
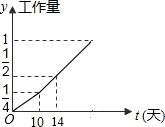 甲、乙两个工程队完成某项工程,首先是甲单独做了10天,然后乙队加入合做,完成剩下的全部工程,设工程总量为单位1,工程进度满足如图所示的函数关系,那么实际完成这项工程所用的时间比由甲单独完成这项工程所需时间少( )
甲、乙两个工程队完成某项工程,首先是甲单独做了10天,然后乙队加入合做,完成剩下的全部工程,设工程总量为单位1,工程进度满足如图所示的函数关系,那么实际完成这项工程所用的时间比由甲单独完成这项工程所需时间少( )| A. | 12天 | B. | 14天 | C. | 16天 | D. | 18天 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
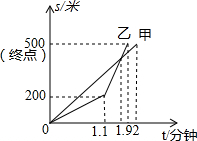 在2015年聊城市举办的“划龙舟,庆端午”比赛中,甲、乙两队在比赛时的路程s(米)与时间t(分钟)之间的函数关系图象如图所示,根据图象得到下列结论,其中错误的是( )
在2015年聊城市举办的“划龙舟,庆端午”比赛中,甲、乙两队在比赛时的路程s(米)与时间t(分钟)之间的函数关系图象如图所示,根据图象得到下列结论,其中错误的是( )| A. | 这次比赛的全程是500米 | |
| B. | 乙队先到达终点 | |
| C. | 比赛中两队从出发到1.1分钟时间段,乙队的速度比甲队的速度快 | |
| D. | 乙与甲相遇时乙的速度是375米/分钟 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com