
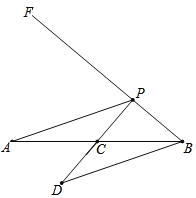
ЁОЬтФПЁПШчЭМЃЌвбжЊЯпЖЮABЃН6cmЃЌЙ§ЕуBзіЩфЯпBFЧвТњзуЁЯABFЃН40ЁуЃЌЕуCЮЊЯпЖЮABжаЕуЃЌЕуPЮЊЩфЯпBFЩЯЕФЖЏЕуЃЌСЌНгPAЃЌЙ§ЕуBзїPAЕФЦНааЯпНЛЩфЯпPCгкЕуDЃЌЩшPBЕФГЄЖШЮЊxcmЃЌPDЕФГЄЖШЮЊy1cmЃЌBDЕФГЄЖШЮЊy2cmЃЎЃЈЕБЕуPгыЕуBжиКЯЪБЃЌy1гыy2ЕФжЕОљЮЊ6cmЃЉ
аЁЬкИљОнбЇЯАКЏЪ§ЕФОбщЃЌЗжБ№ЖдКЏЪ§y1ЃЌy2ЫцздБфСПxЕФБфЛЏЖјБфЛЏЕФЙцТЩНјааСЫЬНОПЃЎ
ЯТУцЪЧаЁЬкЕФЬНОПЙ§ГЬЃЌЧыВЙГфЭъећЃК
ЃЈ1ЃЉАДееЯТБэжаздБфСПx ЃЈ0ЁмxЁм6ЃЉЕФжЕНјааШЁЕуЁЂЛЭМЁЂВтСПЃЌЗжБ№ЕУЕНСЫy1ЃЌy2гыxЕФМИзщЖдгІжЕЃК
x/cm | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
y1/cm | 6.0 | 4.7 | 3.9 | 4.1 | 5.1 | 6.6 | 8.4 |
y2/cm | 6.0 | 5.3 | 4.7 | 4.2 | 3.9 | 4.1 |
ЃЈЫЕУїЃКВЙШЋБэИёЪБЯрЙиЪ§жЕБЃСєвЛЮЛаЁЪ§ЃЉ
ЃЈ2ЃЉдкЭЌвЛЦНУцжБНЧзјБъЯЕxOyжаЃЌУшГіВЙШЋКѓЕФБэжаИїзщЪ§жЕЫљЖдгІЕФЕуЃЈxЃЌy1ЃЉЃЌЃЈxЃЌy2ЃЉЃЌВЂЛГіy1ЃЌy2ЕФЭМЯѓЃЛ
ЃЈ3ЃЉНсКЯКЏЪ§ЭМЯѓНтОіЮЪЬтЃКЕБЁїPDBЮЊЕШбќШ§НЧаЮЪБЃЌдђBPЕФГЄЖШдМЮЊЁЁ ЁЁcmЃЛ
ЃЈ4ЃЉЕБxЃО6ЪБЃЌЪЧЗёДцдкxЕФжЕЪЙЕУЁїPDBЮЊЕШбќШ§НЧаЮЁЁ ЁЁЃЈЬюЁАЪЧЁБЛђепЁАЗёЁБЃЉЃЎ
ЁОД№АИЁПЃЈ1ЃЉy2Ёж3.9ЃЛЃЈ2ЃЉМћНтЮіЃЛЃЈ3ЃЉ3.1Лђ3.9ЃЛЃЈ4ЃЉЗёЃЌРэгЩМћНтЮі
ЁОНтЮіЁП
ЃЈ1ЃЉЛЭМЃЌВтСПМДПЩЕУЃЛ
ЃЈ2ЃЉИљОнЬтЃЈ1ЃЉБэЕФЪ§ОнЃЌдкЭЌвЛЦНУцжБНЧзјБъЯЕ![]() жаЃЌЯШУшЕуЃЌдйЫГДЮСЌНгИїЕуМДПЩЃЛ
жаЃЌЯШУшЕуЃЌдйЫГДЮСЌНгИїЕуМДПЩЃЛ
ЃЈ3ЃЉНсКЯЬтЃЈ2ЃЉЕФЭМЯѓЃЌЗж![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() Ш§жжЧщПіЬжТлМДПЩЕУЃЛ
Ш§жжЧщПіЬжТлМДПЩЕУЃЛ
ЃЈ4ЃЉНсКЯЬтЃЈ2ЃЉЕФЭМЯѓЃЌЗжЮіЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ЕФЭМЯѓЃЌ
ЕФЭМЯѓЃЌ![]() ЕФЭМЯѓЃЌжБЯп
ЕФЭМЯѓЃЌжБЯп![]() Ш§епЪЧЗёгаНЛЕуМДПЩЕУГіД№АИ.
Ш§епЪЧЗёгаНЛЕуМДПЩЕУГіД№АИ.
ЃЈ1ЃЉгЩЛЭМЁЂВтСППЩЕУЃЌ![]() ЪБЃЌ
ЪБЃЌ![]() ЃЛ
ЃЛ
ЃЈ2ЃЉИљОнЬтЃЈ1ЃЉБэЕФЪ§ОнЃЌдкЭЌвЛЦНУцжБНЧзјБъЯЕ![]() жаЃЌЯШУшЕуЃЌдйЫГДЮСЌНгИїЕуЃЌЕУЕНЕФЭМЯѓШчЯТЭМЫљЪОЃК
жаЃЌЯШУшЕуЃЌдйЫГДЮСЌНгИїЕуЃЌЕУЕНЕФЭМЯѓШчЯТЭМЫљЪОЃК

ЃЈ3ЃЉгЩ![]() гы
гы![]() ЕФНЛЕуЕФКсзјБъПЩжЊЃЌ
ЕФНЛЕуЕФКсзјБъПЩжЊЃЌ![]() ЪБЃЌ
ЪБЃЌ![]() ЃЌМД
ЃЌМД![]() ЃЌДЫЪБ
ЃЌДЫЪБ![]() ЮЊЕШбќШ§НЧаЮ
ЮЊЕШбќШ§НЧаЮ
гЩжБЯп![]() гы
гы![]() ЕФНЛЕуЕФКсзјБъПЩжЊЃЌ
ЕФНЛЕуЕФКсзјБъПЩжЊЃЌ![]() ЪБЃЌ
ЪБЃЌ![]() ЃЌМД
ЃЌМД![]() ЃЌДЫЪБ
ЃЌДЫЪБ![]() ЮЊЕШбќШ§НЧаЮ
ЮЊЕШбќШ§НЧаЮ
ЙлВьЭМЯѓПЩжЊЃЌPBВЛПЩФмЕШгкPD
ЙЪД№АИЮЊ3.1Лђ3.9ЃЛ
ЃЈ4ЃЉЙлВьЭМЯѓПЩжЊЃЌЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ЕФЭМЯѓЃЌ
ЕФЭМЯѓЃЌ![]() ЕФЭМЯѓЃЌжБЯп
ЕФЭМЯѓЃЌжБЯп![]() Ш§епУЛгаНЛЕу
Ш§епУЛгаНЛЕу
дђ![]() ВЛПЩФмЮЊЕШбќШ§НЧаЮ
ВЛПЩФмЮЊЕШбќШ§НЧаЮ
ЙЪД№АИЮЊЁАЗёЁБ.



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЯхбєЪаОЋзМЗіЦЖЙЄзївбНјШыЙЅМсНзЖЮЃЎЦЖРЇЛЇеХДѓвЏдкФГЕЅЮЛЕФАяЗіЯТЃЌАбвЛЦЌЦТЕиИФдьКѓжжжВСЫгХжЪЫЎЙћРЖнЎЃЌНёФъе§ЪНЩЯЪаЯњЪлЃЎдкЯњЪлЕФ30ЬьжаЃЌЕквЛЬьТєГі20ЧЇПЫЃЌЮЊСЫРЉДѓЯњСПЃЌВЩШЁСЫНЕМлДыЪЉЃЌвдКѓУПЬьБШЧАвЛЬьЖрТєГі4ЧЇПЫЃЎЕкxЬьЕФЪлМлЮЊyдЊ/ЧЇПЫЃЌyЙигкxЕФКЏЪ§НтЮіЪНЮЊ![]() ЧвЕк12ЬьЕФЪлМлЮЊ32дЊ/ЧЇПЫЃЌЕк26ЬьЕФЪлМлЮЊ25дЊ/ЧЇПЫЃЎвбжЊжжжВЯњЪлРЖнЎЕФГЩФОЪЧ18дЊ/ЧЇПЫЃЌУПЬьЕФРћШѓЪЧWдЊЃЈРћШѓ=ЯњЪлЪеШыЉГЩБОЃЉЃЎ
ЧвЕк12ЬьЕФЪлМлЮЊ32дЊ/ЧЇПЫЃЌЕк26ЬьЕФЪлМлЮЊ25дЊ/ЧЇПЫЃЎвбжЊжжжВЯњЪлРЖнЎЕФГЩФОЪЧ18дЊ/ЧЇПЫЃЌУПЬьЕФРћШѓЪЧWдЊЃЈРћШѓ=ЯњЪлЪеШыЉГЩБОЃЉЃЎ
ЃЈ1ЃЉm=ЁЁ ЁЁЃЌn=ЁЁ ЁЁЃЛ
ЃЈ2ЃЉЧѓЯњЪлРЖнЎЕкМИЬьЪБЃЌЕБЬьЕФРћШѓзюДѓЃПзюДѓРћШѓЪЧЖрЩйЃП
ЃЈ3ЃЉдкЯњЪлРЖнЎЕФ30ЬьжаЃЌЕБЬьРћШѓВЛЕЭгк870дЊЕФЙВгаЖрЩйЬьЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПзд2016ФъЙВЯэЕЅГЕЩЯЪавдРД,ИјШЫУЧЕФГіааЬсЙЉСЫСЫБуРћ,ЪмЕНСЫЙуДѓЪаУёЕФЧрэљЃЌФГЙЋЫОЮЊСЫСЫНтдБЙЄЩЯЯТАрЛиМвЕФТЗЯпЃЈЩшТЗГЬЮЊxЙЋРяЃЉЧщПіЃЌЫцЛњГщШЁСЫШєИЩУћдБЙЄНјааСЫЮЪОэЕїВщ,ЯжНЋетаЉдБЙЄЕФЮНВщНсЙћЗжЮЊЫФИіЕШМЖЃЌAЃК0ЁмxЁм3ЁЂBЃК3ЃМxЁм6ЁЂCЃК6ЃМxЁм9ЁЂDЃКxЃО9,ВЂНЋЕїВщНсЙћЛцжЦГЩШчЯТСНИіВЛЭъећЕФЭГМЦЭМЁЃ
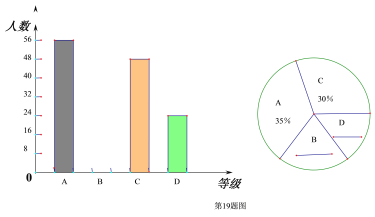
ЃЈ1ЃЉВЙШЋЩЯУцЕФЬѕаЮЭГМЦЭМКЭЩШаЮЭГМЦЭМжаЕФB D ЃЛ
ЃЈ2ЃЉЫљГщШЁдБЙЄЯТАрТЗГЬЕФжаЮЛЪ§ТфдкЕШМЖ ЃЈЬюзжФИ)
ЃЈ3ЃЉШєИУЙЋЫОга900УћдБЙЄ,ЮЊСЫЗНБудБЙЄЩЯЯТАр,дкИпЗхЦкЪБЙцЖЈТЗГЬдк6ЙЋРявдЩЯПЩгХЯШбЁдёЙВЯэЕЅГЕЯТАп,ЧыФуЙРЫуИУЙЋЫОгаЖрЩйШЫПЩвдгХЯШбЁдёЙВЯэЕЅГЕЁЃ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЙигкxЕФвЛдЊЖўДЮЗНГЬaЃЈxЉh+1ЃЉ2+k+2ЃН0ЃЈaЃО0ЃЉЕФНтЪЧx1ЃНЉ5ЃЌx2ЃН1ЃЌдђВЛЕШЪНaЃЈx+hЉ2ЃЉ2+kЃМЉ2ЕФНтМЏЮЊ_____ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЮЊСЫСЫНтбЇЩњУПдТЕФСугУЧЎЧщПіЃЌДгМзЁЂввЁЂБћШ§ИібЇаЃИїЫцЛњГщШЁ200УћбЇЩњЃЌЕїВщСЫЫћУЧЕФСугУЧЎЧщПіЃЈЕЅЮЛЃКдЊЃЉОпЬхЧщПіШчЯТЃК
бЇаЃЦЕЪ§СугУЧЎ | 100ЁмxЃМ200 | 200ЁмxЃМ300 | 300ЁмxЃМ400 | 400ЁмxЃМ500 | 500вдЩЯ | КЯМЦ |
Мз | 5 | 35 | 150 | 8 | 2 | 200 |
вв | 16 | 54 | 68 | 52 | 10 | 200 |
Бћ | 0 | 10 | 40 | 70 | 80 | 200 |
дкЕїВщЙ§ГЬжаЃЌДг__ЃЈЬюЁАМзЁБЃЌЁАввЁБЛђЁАБћЁБЃЉаЃЫцЛњГщШЁбЇЩњЃЌГщЕНЕФбЇЩњЁАСугУЧЎВЛЕЭгк300дЊЁБЕФПЩФмадзюДѓЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПаЁдЊВНааДгМвШЅЛ№ГЕеОЃЌзпЕН 6 ЗжжгЪБЃЌвдЭЌбљЕФЫйЖШЛиМвШЁЮяЦЗЃЌШЛКѓДгМвГЫГізтГЕИЯЭљЛ№ГЕеОЃЌНсЙћБШдЄМЦВНааЪБМфЬсЧАСЫ3 ЗжжгЃЎаЁдЊРыМвТЗГЬS(Уз)гыЪБМфt(Зжжг)жЎМфЕФКЏЪ§ЭМЯѓШчЭМЃЌДгМвЕНЛ№ГЕеОТЗГЬЪЧ( )
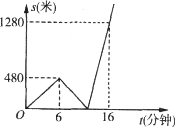
A.1300 УзB.1400 УзC.1600 УзD.1500 Уз
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЃКЫФБпаЮ ABCD ФкНггкЁбOЃЌСЌНг ACЁЂBDЃЌЁЯBAD+2ЁЯACB=180ЁуЃЎ
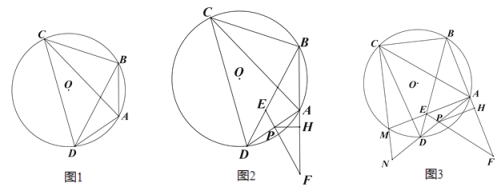
ЃЈ1ЃЉШчЭМ 1ЃЌЧѓжЄЃКЕу A ЮЊЛЁ BD ЕФжаЕуЃЛ
ЃЈ2ЃЉШчЭМ 2ЃЌЕу E ЮЊЯв BD ЩЯвЛЕуЃЌбгГЄ BA жСЕу FЃЌЪЙЕУ AF=ABЃЌСЌНг FE НЛ AD гкЕу PЃЌЙ§Еу P зї PHЁЭAF гкЕу HЃЌAF=2AH+APЃЌЧѓжЄЃКAH:AB=PE:BEЃЛ
ЃЈ3ЃЉдкЃЈ2ЃЉЕФЬѕМўЯТЃЌШчЭМ 3ЃЌСЌНг AEЃЌВЂбгГЄ AE НЛЁбO гкЕу MЃЌСЌНг CMЃЌВЂбгГЄ CM НЛ AD ЕФбгГЄЯпгкЕу NЃЌСЌНг FDЃЌЁЯMND=ЁЯMEDЃЌDF=12ЉqsinЁЯACBЃЌMN=![]() ЃЌЧѓ AH ЕФГЄЃЎ
ЃЌЧѓ AH ЕФГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЁїABCжаЃЌACЃНBCЃЌЁЯACBЃН90ЁуЃЌЕуDдкБпBCЩЯЃЌBDЃН6ЃЌCDЃН2ЃЌЕуPЪЧБпABЩЯвЛЕуЃЌдђPCЃЋPDЕФзюаЁжЕЮЊ___.
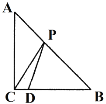
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвбжЊЖўДЮКЏЪ§yЃНЃ![]() x2ЃЋ4xЃ6ЃЎ
x2ЃЋ4xЃ6ЃЎ
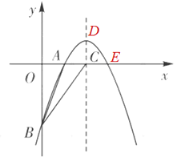
ЃЈ1ЃЉжБНгаДГіХзЮяЯпгызјБъжсЕФНЛЕузјБъЃЛ
ЃЈ2ЃЉЩшЖўДЮКЏЪ§ЕФЖдГЦжсгыxжсНЛгкЕуCЃЌСЌНгBAЃЌBCЃЌЧѓЁїABCЕФУцЛ§ЃЛ
ЃЈ3ЃЉШєХзЮяЯпЕФЖЅЕуЮЊDЃЌдкyжсЩЯЪЧЗёДцдквЛЕуPЃЌЪЙЕУЁїPADЕФжмГЄзюаЁЃПШєДцдкЃЌЧѓГіЁїPADЕФжмГЄЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com