练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    如图，在△ABC中，DE∥BC，
    AE
    EC
    =
    1
    2
    ，求△DOE与△BOC周长比与面积比．
    考点：相似三角形的判定与性质
    专题：
    分析：由条件可证明△DOE∽△COB，根据
    AE
    EC
    =
    1
    2
    ，可求得其相似比，再根据相似三角形的性质可求得答案．
    解答：解：∵
    AE
    EC
    =
    1
    2
    ，
    ∴
    AE
    AC
    =
    1
    3
    ，
    ∵DE∥BC，
    ∴∠DEO=∠OBC，∠EDO=∠OCB，
    ∴△DOE∽△COB，且
    DE
    BC
    =
    AE
    AC
    =
    1
    3
    ，
    ∴
    C△DOE
    C△BOC
    =
    DE
    BC
    =
    1
    3
    ，
    S△DOE
    S△BOC
    =（
    DE
    BC
    ）2=（
    1
    3
    ）2=
    1
    9
    ．
    点评：本题主要考查相似三角形的判定和性质，掌握相似三角形的周长比等于相似比、面积比等于相似比的平方是解题的关键．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    求x：
    3
    x-2
    =2-
    2x
    x+2
    ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

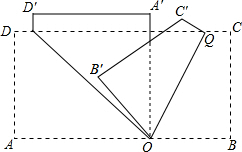    要用一张长方形纸折成一个纸袋，两条折痕的夹角为70°（即∠POQ=70°），将折过来的重叠部分抹上胶水，即可做成一个纸袋，则粘胶水部分所构成的角，∠A′OB′=
     
    °．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    若点C、D在线段AB上，且C为AB的一个三等分点，D为AC的中点，若BC=2，则BD的长为
     
    ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

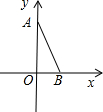    如图，在平面直角坐标系中，A（0，4），B（2，0），点C在第一象限，若以A、B、C为顶点的三角形与△AOB相似（不包括全等），则点C的个数是（　　）
    A、1B、2C、3D、4

    查看答案和解析>>

    科目：初中数学 来源： 题型：

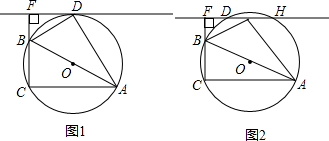    如图，AB为⊙O直径．C，D为⊙O上一点，F为CB延长线上一点，且
    BC
    =
    BD
    ，AC=2
    		3
    ．
    （1）如图1，DF⊥CF，BC=2，证明：DF与⊙O相切；
    （2）如图2，H为⊙O上的一点，若
    BD
    =
    DH
    ，DH⊥CF于F，求BC的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    在平面直角坐标系中，二次函数y=-x2+bx+c的图象与x轴交与点A（-1，0）B（4，0），且与y轴相交于C，在第一象限内抛物线上是否存在D，使得∠ADB=45°？若存在，求出点D坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    把一个长方形（对边平行且相等，每一个角均为直角）纸片按图进行折叠，使顶点B和D重合，折痕为EF．请问△A′ED与△CFD全等吗？若全等，请证明．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    计算：
    cos45°-sin30°
    cos60°+
    1
    2
    tan45°
    ．

    查看答案和解析>>

    同步练习册答案