

分析 (1)由含30°角的直角三角形的性质得出BC=2AB=6,∠ABC=60°,求出∠CBD=∠NBP=60°,证出∠ACB=∠CBD,由角平分线的性质和勾股定理即可得出答案;
(2)证明A、B、D、C四点共圆,由圆周角定理得出∠CBD=∠CAD,∠NBP=∠DCA,由∠CBD=∠NBP,得出∠DCA=∠CAD,即可得出结论;
(3)由三角形的外角性质证出∠AEB=∠DAE,得出DE=AD=CD,设BF=x,作DE⊥AC于E,DF⊥AN于F,则DF=AE=$\frac{1}{2}$AC=2,由勾股定理求出BC=5,证明△BCD∽△BDF,得出BD2=BC•BF=5x,再由勾股定理得出方程,解方程求出x,即可得出结论.
解答 (1)解:∵∠ACB=30°,∠MAN=90°,AB=3,
∴BC=2AB=6,∠ABC=60°,
∴∠CBN=180°-60°=120°,
∵BP平分∠CBN,
∴∠CBD=∠NBP=60°,
∴∠ACB=60°=∠CBD,
∵CD⊥BP,∠MAN=90°,
∴CD=CA=$\sqrt{3}$AB=3$\sqrt{3}$;
故答案为:3$\sqrt{3}$;
(2)证明:∵∠CDB=∠MAN=90°,
∴∠CDB+∠MAN=180°,
∴A、B、D、C四点共圆,
∴∠CBD=∠CAD,∠NBP=∠DCA,
∵∠CBD=∠NBP,
∴∠DCA=∠CAD,
∴AD=CD;
(3)解:∵AE平分∠MAN,∠MAN=90°,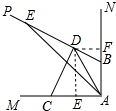
∴∠MAE=∠NAE=45°,
∵∠NBE=∠BAE+∠AEB,∠DAC=∠MAE+∠DAE,
∴∠AEB=∠DAE,
∴DE=AD=CD,
设BF=x,作DE⊥AC于E,DF⊥AN于F,
则DF=AE=$\frac{1}{2}$AC=2,
∵∠MAN=90°,
∴BC=$\sqrt{A{B}^{2}+A{C}^{2}}$=$\sqrt{{3}^{2}+{4}^{2}}$=5,
∵∠CDB=∠DFB=90°,∠CBD=∠NBP,
∴△BCD∽△BDF,
∴BD:BF=BC:BD,
∴BD2=BC•BF=5x,
∵AD2=BC2-BD2,AD2=DF2+AF2,AD=CD,
∴BC2-BD2=DF2+AF2,
即52-5x=22+(3+x)2,
解得:x=1,或x=-12(舍去),
∴x=1,
∴AD2=25-5=20,
∴DE=AD=$\sqrt{20}$=2$\sqrt{5}$.
点评 本题是三角形综合题目,考查了含30°角的直角三角形的性质、四点共圆、圆周角定理、等腰三角形的判定、三角形的外角性质、勾股定理、相似三角形的判定与性质等知识;本题综合性强,难度较大,特别是(3)中,需要通过作辅助线运用勾股定理得出方程才能得出结果.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:选择题
| A. | 赚了12元 | B. | 亏了12元 | C. | 赚了20元 | D. | 亏了20元 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com